Câu 16 trang 51 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABCD. Gọi M là một điểm nằm trong tam giác SCD
Đề bài
Cho hình chóp S.ABCD. Gọi M là một điểm nằm trong tam giác SCD
a. Tìm giao tuyến của hai mặt phẳng (SMB) và (SAC)
b. Tìm giao điểm của đường thẳng BM và mp(SAC)
c. Xác định thiết diện của hình chóp khi cắt bởi mp(ABM)
Lời giải chi tiết
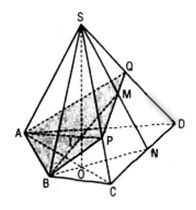
a. Tìm (SBM) ∩ (SAC)
Dễ thấy \(S \in \left( {SBM} \right) \cap \left( {SAC} \right)\)
Trong (SCD), gọi N = SM ∩ CD
Trong mp(ABCD) gọi O = BN ∩ AC
\( \Rightarrow \left\{ \begin{array}{l} O \in BN \subset \left( {SBM} \right)\\ O \in AC \subset \left( {SAC} \right) \end{array} \right. \)\(\Rightarrow O \in \left( {SBM} \right) \cap \left( {SAC} \right)\)
Vậy SO = (SBM) ∩ (SAC)
b. Tìm BM ∩ (SAC)
Chọn mặt phẳng phụ chứa BM là (SBN)
Ta có: (SBN) ∩ (SAC) = SO (theo câu a)
Gọi I = SO ∩ BM thì
\(\left\{ \begin{array}{l} I \in SO \subset \left( {SAC} \right)\\ I \in BM \end{array} \right. \)\(\Rightarrow I = BM \cap \left( {SAC} \right)\)
c. Trong mp(SAC) gọi P = AI ∩ SC
Trong mp(SCD), PM cắt SD tại Q.
Thiết diện của hình chóp khi cắt bởi mp(ABM) là tứ giác ABPQ.