Đề kiểm tra 15 phút - Đề số 1 - Bái 2 - Chương 3 - Hình học 9 — Không quảng cáo

Đề bài

Cho ∆ABC đều. Trên nửa mặt phẳng bờ BC không chứa điểm A. Vẽ nửa đường tròn đường kính BC. Lấy D, E trên nửa đường tròn sao cho $\overparen{ BD} = \overparen{ DE} = \overparen{ EC}$.  Gọi I, J lần lượt là giao điểm của AD, AE với BC. Chứng minh rằng: $BI = IJ = JC.$

Lời giải chi tiết

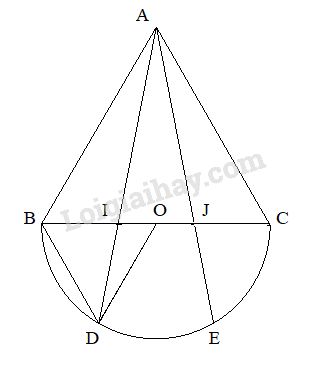
Ta có: $\overparen{ BD} = \overparen{ DE} = \overparen{EC}$ (gt)

$\Rightarrow sđ\overparen{BD} = sđ\overparen{DE} = sđ\overparen{ EC} =60^o$

Do đó ∆BOD đều ( cân có một góc 60º)

$\Rightarrow \widehat {OBD} = 60^\circ$

Xét $∆BID$ và $∆CIA$ có :

$\widehat {BID} = \widehat {CIA}$ ( đối đỉnh)

$\widehat {OBD} = \widehat {ICA} = 60^\circ$

Vậy ∆BID đồng dạng với ∆CIA (g.g)

$\Rightarrow \dfrac{{BI} }{ {CI}} = \dfrac{{BD} }{ {CA}} =\dfrac {{OB} }{ {BC}} = \dfrac{1 }{ 2}$ ( vì $BD = OB$ và $CA = BC$)

$\Rightarrow BI =\dfrac {1 }{ 3}BC$.

Tương tự, ta chứng minh được$CJ =\dfrac {1 }{ 3}BC.$

Do đó: $BI = IJ = JC.$