Đề kthi học kì 2 - Đề số 5
Đề bài

Lan nói: “trong hai phân số (khác \(0\)) có tử số bằng nhau, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn”. Theo em, Lan nói đúng hay sai ?
A. Đúng
B. Sai

Thực hiện tính:
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Một cửa hàng có \(360m\) vải hoa và vải màu, trong đó số mét vải hoa ít hơn số mét vải màu là \(24m\).
Vậy cửa hàng có
mét vải hoa.
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Hiệu của hai số là \(57\). Tỉ số của hai số đó là \(\dfrac{2}{5}\).
Vậy số bé là
 Kết quả của phép chia \(90405:45\) là:
Kết quả của phép chia \(90405:45\) là:
A. \(29\)
B. \(209\)
C. \(2009\)
D. \(2090\)
Biểu đồ dưới đây nói về các môn thể thao khối lớp Bốn tham gia:
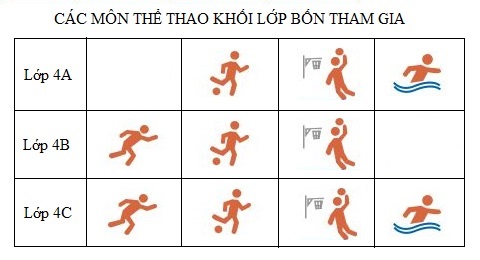
Hỏi lớp 4A tham gia mấy môn thể thao, gồm những môn nào?
A. \(4\) môn, đó là chạy, bóng đá, bóng chuyền, bơi
B. \(3\) môn, đó là bóng đá, bóng rổ, bơi.
C. \(3\) môn, đó là chạy, bóng đá, bóng rổ.
D. \(2\) môn, đó là chạy, bóng rổ.

Một người đã bán được \(324\) quả cam và quýt , trong đó số cam bằng \(\dfrac{4}{5}\) số quýt. Tính số cam, số quýt đã bán.
A. \(134\) quả cam; \(190\) quả quýt
B. \(140\) quả cam; \(175\) quả quýt
C. \(136\) quả cam; \(185\) quả quýt
D. \(144\) quả cam; \(180\) quả quýt

Điền số thích hợp vào ô trống:
Hình thoi có độ dài các đường chéo là \(37dm\) và \(4m\) có diện tích là:
\(dm^2\).

Điền số thích hợp vào ô trống:
Số trung bình cộng của các số $27;{\rm{ 45}}$ là

Quy đồng mẫu số của phân số \(\dfrac{2}{3}\) và \(\dfrac{1}{4}\) ta được phân số \(\dfrac{8}{{12}}\) và phân số \(...\).
Phân số thích hợp điền vào chỗ chấm là:
A. \(\dfrac{3}{{12}}\)
B. \(\dfrac{4}{{12}}\)
C. \(\dfrac{5}{{12}}\)
D. \(\dfrac{6}{{12}}\)

Trong các hình sau, hình nào là hình thoi?
A.
B.
C.

D.

 Tỉ số của \(3\) và \(8\) là:
Tỉ số của \(3\) và \(8\) là:
A. \(3:8\)
B. \(\dfrac{3}{8}\)
C. Cả A và B đều đúng
D. Cả A và B đều sai
 Phép cộng các số tự nhiên có những tính chất nào dưới đây?
Phép cộng các số tự nhiên có những tính chất nào dưới đây?
A. Tính chất giao hoán
B. Tính chất kết hợp
C. Tính chất cộng với số \(0\)
D. Tất cả các đáp án trên đều đúng

Điền số thích hợp vào ô trống:

Rút gọn phân số sau thành phân số tối giản:

Tính: \(5 + \dfrac{2}{9}\)
A. \(\dfrac{7}{9}\)
B. \(\dfrac{{43}}{9}\)
C. \(\dfrac{{47}}{9}\)
D. \(\dfrac{{52}}{9}\)

Điền số thích hợp vào ô trống:
Một hình chữ nhật có chiều rộng là \(35dm\). Như vậy chiều rộng bằng $\dfrac{5}{7}$ chiều dài.
Vậy diện tích hình chữ nhật đó là
\(cm^2\).
Nối kết quả với phép tính tương ứng:
\(\dfrac{5}{6} + \dfrac{5}{8}\)
\(\dfrac{{27}}{{32}} \times \dfrac{4}{9}\)
\(\dfrac{7}{6} - \dfrac{3}{4}\)
\(\dfrac{{25}}{4}:3\)
\(\dfrac{{25}}{{12}}\)
\(\dfrac{3}{8}\)
\(\dfrac{{35}}{{24}}\)
\(\dfrac{5}{{12}}\)
Chọn đáp án đúng hoặc sai cho mỗi khẳng định bên dưới:
Trong hình thoi MNPQ:
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Tổng của hai số là \(765\), nếu giảm số lớn đi \(4\) lần thì ta được số bé.
Vậy hiệu của hai số đó là
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Một hình chữ nhật có chu vi là \(468cm\). Biết chiều rộng bằng \(\dfrac{5}{8}\) chiều dài.
Vậy diện tích hình chữ nhật đó là
\(c{m^2}\).
 Tính giá trị biểu thức: \(5 - \dfrac{3}{8}:\dfrac{5}{{12}}\)
Tính giá trị biểu thức: \(5 - \dfrac{3}{8}:\dfrac{5}{{12}}\)
A. \(\dfrac{{111}}{{10}}\)
B. \(\dfrac{{41}}{{10}}\)
C. \(\dfrac{{35}}{{24}}\)
D. \(\dfrac{{155}}{{32}}\)

Điền số thích hợp vào ô trống:
Có \(2\) xe tải lớn, mỗi xe chở được \(4525kg\) gạo và \(3\) xe tải nhỏ, mỗi xe chở được $3600kg$ gạo.
Vậy trung bình mỗi xe tải chở được
\(kg\) gạo.

Giá trị của biểu thức \(\dfrac{3}{4} - \dfrac{2}{5} \times \dfrac{7}{8}\) là:
A. \(\dfrac{1}{4}\)
B. \(\dfrac{2}{5}\)
C. \(\dfrac{4}{5}\)
D. \(\dfrac{{49}}{{160}}\)

Một mảnh đất hình chữ nhật có chiều dài \(27m\), chiều rộng bằng \(\dfrac{2}{3}\) chiều dài. Người ta sử dụng \(\dfrac{5}{9}\) diện tích để trồng hoa, \(\dfrac{1}{6}\) diện tích để làm đường đi và phần diện tích còn lại để xây bể nước. Tính diện tích phần xây bể nước.
A. \(81{m^2}\)
B. \(486{m^2}\)
C. \(270{m^2}\)
D. \(135{m^2}\)
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Hiệu của hai số là \(882\). Số thứ nhất là số tròn chục và nếu xóa đi chữ số \(0\) ở bên phải số thứ nhất thì được số thứ hai.
Vậy số thứ nhất là
, số thứ hai là
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Tổng số học sinh của trường Hoàng Diệu và trường Lê Lợi là \(1275\) học sinh. Nếu chuyển \(54\) học sinh từ trường Hoàng Diệu sang trường Lê Lợi thì trường Lê Lợi có nhiều hơn trường Hoàng Diệu \(35\) học sinh.
Vậy lúc đầu trường Hoàng Diệu có
học sinh,
trường Lê Lợi có
học sinh.

Điền số thích hợp vào ô trống:
Trong đợt kiểm tra học kì I vừa qua ở lớp 4A thầy giáo nhận thấy \(\dfrac{1}{2}\) số học sinh đạt điểm giỏi, \(\dfrac{2}{5}\) số học sinh đạt điểm khá, \(4\) học sinh đạt điểm trung bình và không có học sinh nào đạt điểm yếu.
Vậy lớp 4A có
học sinh đạt điểm giỏi,
học sinh đạt điểm khá.

Có thể viết được bao nhiêu phân số từ ba chữ số \(2\,;\,\,4\,;\,\,7\), trong đó tử số và mẫu số là các số có một chữ số và tử số khác mẫu số?
A. \(6\) số
B. \(7\) số
C. \(8\) số
D. \(9\) số
 Điền số thích hợp vào ô trống :
Điền số thích hợp vào ô trống :
Sân trường của trường tiểu học Kim Đồng dạng hình chữ nhật có chiều dài \(75m\), chiều rộng \(45m\) được vẽ trên bản đồ tỉ lệ \(1:1500\).
Vậy trên bản đồ, chu vi của sân trường đó là
\(cm\).
Lời giải và đáp án

Lan nói: “trong hai phân số (khác \(0\)) có tử số bằng nhau, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn”. Theo em, Lan nói đúng hay sai ?
A. Đúng
B. Sai
A. Đúng
B. Sai
Trong hai phân số có cùng tử số:
+) Phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
+) Phân số nào có mẫu số lớn hơn thì phân số đó bé hơn.
+) Nếu mẫu số bằng nhau thì hai phân số đó bằng nhau.
Vậy Lan nói đúng.

Thực hiện tính:
Áp dụng quy tắc nhân hai phân số: Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
Ta có: \(\dfrac{3}{5} \times \dfrac{4}{7} = \dfrac{{3 \times 4}}{{5 \times 7}} = \dfrac{{12}}{{35}}\)
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(12\,;\,\,35\).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Một cửa hàng có \(360m\) vải hoa và vải màu, trong đó số mét vải hoa ít hơn số mét vải màu là \(24m\).
Vậy cửa hàng có
mét vải hoa.
Một cửa hàng có \(360m\) vải hoa và vải màu, trong đó số mét vải hoa ít hơn số mét vải màu là \(24m\).
Vậy cửa hàng có
mét vải hoa.
Coi số mét vải hoa là số bé, ta áp dụng công thức tìm hai số khi biết tổng và hiệu của hai số đó:
Số bé = (tổng – hiệu) : $2$
Ta có sơ đồ:
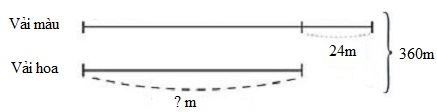
Cửa hàng có số mét vài hoa là:
$(360 - 24):2 = 168\,\,(m)$
Đáp số: \(168m\) ;
Vậy đáp án đúng điền vào ô trống là \(168\).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Hiệu của hai số là \(57\). Tỉ số của hai số đó là \(\dfrac{2}{5}\).
Vậy số bé là
Hiệu của hai số là \(57\). Tỉ số của hai số đó là \(\dfrac{2}{5}\).
Vậy số bé là
Bài toán cho biết hiệu và tỉ số của hai số. Đây là dạng toán tìm hai số khi biết hiệu và tỉ số của 2 số đó.
Theo bài ra tỉ số của hai số đó là \(\dfrac{2}{5}\) nên ta vẽ sơ đồ biểu thị số bé gồm \(2\) phần, số lớn gồm \(5\) phần như thế. Ta tìm số bé theo công thức:
Số bé = (Hiệu : hiệu số phần bằng nhau) × số phần của số bé
Ta có sơ đồ:
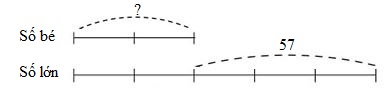
Theo sơ đồ, hiệu số phần bằng nhau là:
\(5 - 2 = 3\) (phần)
Số bé là:
\(57:3 \times 2 = 38\)
Đáp số: \(38\).
Vậy đáp án đúng điền vào ô trống là \(38\).
 Kết quả của phép chia \(90405:45\) là:
Kết quả của phép chia \(90405:45\) là:
A. \(29\)
B. \(209\)
C. \(2009\)
D. \(2090\)
C. \(2009\)
Đặt tính rồi tính, chia theo thứ tự từ trái sang phải.
Ta đặt tính và thực hiện tính như sau:
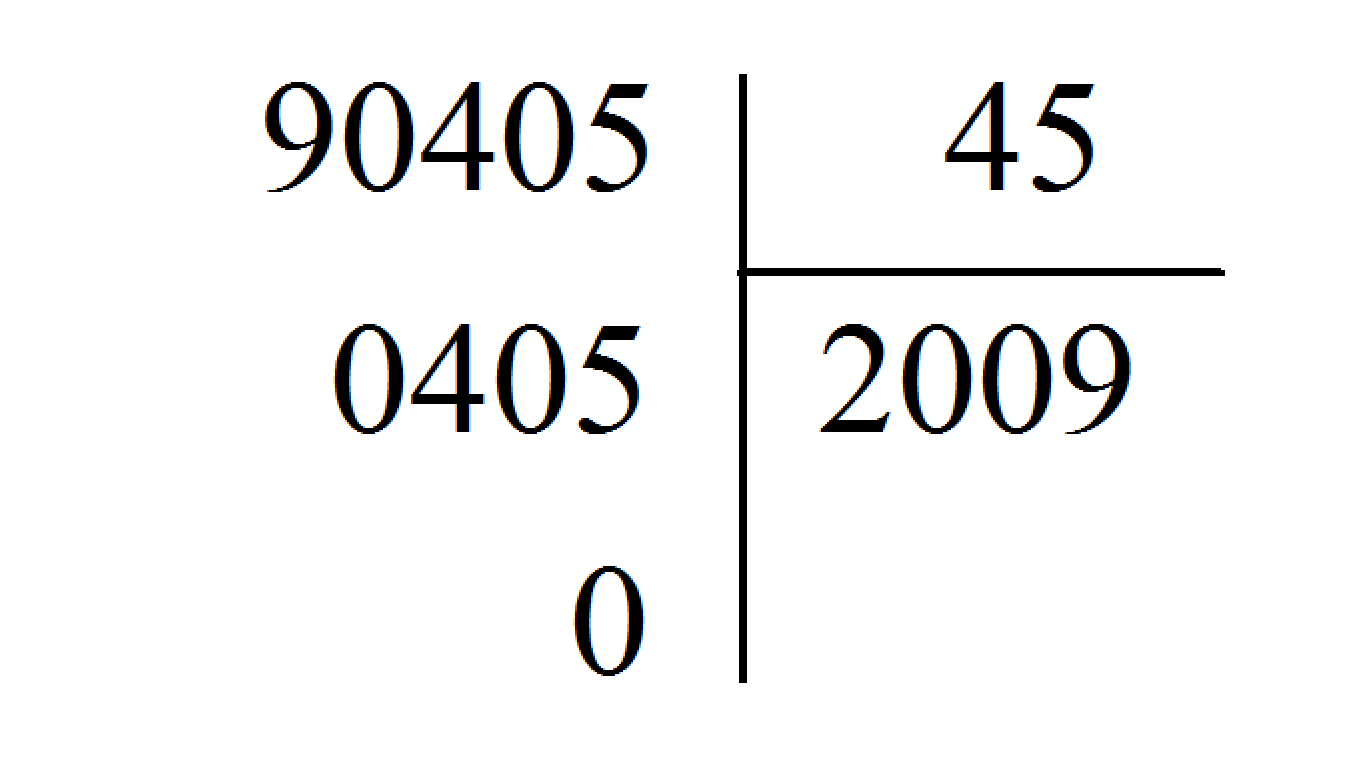
Vậy \(90405:45 = 2009\).
Biểu đồ dưới đây nói về các môn thể thao khối lớp Bốn tham gia:

Hỏi lớp 4A tham gia mấy môn thể thao, gồm những môn nào?
A. \(4\) môn, đó là chạy, bóng đá, bóng chuyền, bơi
B. \(3\) môn, đó là bóng đá, bóng rổ, bơi.
C. \(3\) môn, đó là chạy, bóng đá, bóng rổ.
D. \(2\) môn, đó là chạy, bóng rổ.
B. \(3\) môn, đó là bóng đá, bóng rổ, bơi.
Quan sát biểu đồ, hàng thứ nhất chỉ các môn thể thao lớp 4A tham gia.
Nhìn vào biểu đồ ta thấy lớp 4A tham gia \(3\) môn thể thao, đó là bóng đá, bóng rổ, bơi.

Một người đã bán được \(324\) quả cam và quýt , trong đó số cam bằng \(\dfrac{4}{5}\) số quýt. Tính số cam, số quýt đã bán.
A. \(134\) quả cam; \(190\) quả quýt
B. \(140\) quả cam; \(175\) quả quýt
C. \(136\) quả cam; \(185\) quả quýt
D. \(144\) quả cam; \(180\) quả quýt
D. \(144\) quả cam; \(180\) quả quýt
Bài toán cho biết tổng và tỉ số của số cam và số quýt .
Đây là dạng toán tìm hai số khi biết tổng và tỉ số của 2 số đó.
Theo bài ra số cam bằng \(\dfrac{4}{5}\) số quýt nên ta vẽ sơ đồ biểu thị số cam gồm \(4\) phần, số quýt gồm \(5\) phần như thế. Cọi số cam là số bé, số quýt là số lớn, ta tìm hai số theo công thức:
Số bé = (Tổng : tổng số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (Tổng : tổng số phần bằng nhau) × số phần của số lớn.
Ta có sơ đồ
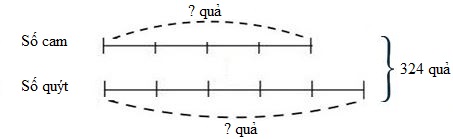
Theo sơ đồ, tổng số phần bằng nhau là:
\(4 + 5 = 9\) (phần)
Số cam đã bán là:
\(324:9 \times 4 = 144\,\,\) (quả)
Số quýt đã bán là:
\(324 - 144 = 180\) (quả)
Đáp số: \(144\) quả cam; \(180\) quả quýt.

Điền số thích hợp vào ô trống:
Hình thoi có độ dài các đường chéo là \(37dm\) và \(4m\) có diện tích là:
\(dm^2\).
Hình thoi có độ dài các đường chéo là \(37dm\) và \(4m\) có diện tích là:
\(dm^2\).
Độ dài hai đường chéo chưa cùng đơn vị đo nên ta đổi về cùng đơn vị đo, sau đó để tính diện tích ta lấy tích độ dài hai đường chéo chia cho \(2\).
Đổi: \(4m = 40dm\).
Diện tích hình thoi đó là:
\(37 \times 40:2 = 740\left( {d{m^2}} \right)\) Đáp số: \(740d{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(740\).

Điền số thích hợp vào ô trống:
Số trung bình cộng của các số $27;{\rm{ 45}}$ là
Số trung bình cộng của các số $27;{\rm{ 45}}$ là
Muốn tìm số trung bình cộng của hai số, ta tính tổng của các số đó, rồi chia tổng đó cho \(2\).
Số trung bình cộng của các số $27;{\rm{ 45}}$ là:
\((27 + 45):2 = 36\)
Vậy đáp án đúng điền vào ô trống là \(36\).

Quy đồng mẫu số của phân số \(\dfrac{2}{3}\) và \(\dfrac{1}{4}\) ta được phân số \(\dfrac{8}{{12}}\) và phân số \(...\).
Phân số thích hợp điền vào chỗ chấm là:
A. \(\dfrac{3}{{12}}\)
B. \(\dfrac{4}{{12}}\)
C. \(\dfrac{5}{{12}}\)
D. \(\dfrac{6}{{12}}\)
A. \(\dfrac{3}{{12}}\)
Khi quy đồng mẫu số hai phân số có thể làm như sau:
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
Chọn \(MSC = 12\)
Quy đồng mẫu số hai phân số \(\dfrac{2}{3}\) và \(\dfrac{1}{4}\) ta được:
\(\dfrac{2}{3} = \dfrac{{2 \times 4}}{{3 \times 4}} = \dfrac{8}{{12}}\,\,\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{4} = \dfrac{{1 \times 3}}{{4 \times 3}} = \dfrac{3}{{12}}\)
Vậy quy đồng mẫu số của phân số \(\dfrac{2}{3}\) và \(\dfrac{1}{4}\) ta được hai phân số \(\dfrac{8}{{12}}\) và \(\dfrac{3}{{12}}\).

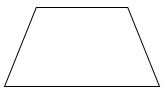
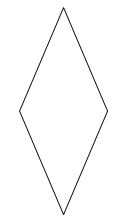
Trong các hình sau, hình nào là hình thoi?
A.

B.

C.

D.

B.

Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Quan sát các hình đã cho ta thấy hình A là hình thang, hình B là hình thoi, hình C là hình tròn, hình D là hình bình hành.
Vậy trong các hình đã cho, hình B là hình thoi.
 Tỉ số của \(3\) và \(8\) là:
Tỉ số của \(3\) và \(8\) là:
A. \(3:8\)
B. \(\dfrac{3}{8}\)
C. Cả A và B đều đúng
D. Cả A và B đều sai
C. Cả A và B đều đúng
Áp dụng định nghĩa : Tỉ số của \(a\) và \(b\) là \(a:b\) hay \(\dfrac{a}{b}\) (\(b\) khác \(0\)).
Tỉ số của \(3\) và \(8\) là \(3:8\) hay \(\dfrac{3}{8}\).
Vậy cả đáp án A và B đều đúng.
Chọn C.
 Phép cộng các số tự nhiên có những tính chất nào dưới đây?
Phép cộng các số tự nhiên có những tính chất nào dưới đây?
A. Tính chất giao hoán
B. Tính chất kết hợp
C. Tính chất cộng với số \(0\)
D. Tất cả các đáp án trên đều đúng
D. Tất cả các đáp án trên đều đúng
Xem lại lí thuyết về các tính chất của phép cộng các số tự nhiên.
Phép cộng các số tự nhiên có tính chất:
- Tính chất giao hoán: Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi.
- Tính chất kết hợp: Khi cộng một tổng hai số với số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba.
- Tính chất cộng với số \(0\): Mọi số tự nhiên cộng với số \(0\) đều bằng chính số đó.
Vậy các đáp án A, B, C đều đúng.

Điền số thích hợp vào ô trống:
Từ định nghĩa : Tỉ số của \(a\) và \(b\) là \(a:b\) hay \(\dfrac{a}{b}\) (\(b\) khác \(0\)), ta suy ra tỉ số của \(b\) và \(a\) là \(b:a\) hay \(\dfrac{b}{a}\).
Với \(a = 11\,;\,\,b = 15\) thì tỉ số của \(b\) và \(a\) là \(15:11\) hay \(\dfrac{{15}}{{11}}\).

Rút gọn phân số sau thành phân số tối giản:
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta chia cả tử số và mẫu số của phân số \(\dfrac{5}{{20}}\) cho \(5\).
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta có:
\(\dfrac{5}{{20}} = \dfrac{{5:5}}{{20:5}} = \dfrac{1}{4}\)
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(1\,;\,\,4\).

Tính: \(5 + \dfrac{2}{9}\)
A. \(\dfrac{7}{9}\)
B. \(\dfrac{{43}}{9}\)
C. \(\dfrac{{47}}{9}\)
D. \(\dfrac{{52}}{9}\)
C. \(\dfrac{{47}}{9}\)
Viết \(5\) dưới dạng phân số là \(\dfrac{5}{1}\) rồi thực hiện phép tính cộng hai phân số.
Ta có: \(5 + \dfrac{2}{9} = \dfrac{5}{1} + \dfrac{2}{9} = \dfrac{{45}}{9} + \dfrac{2}{9} = \dfrac{{47}}{9}\)
Hoặc ta có thể viết gọn như sau: \(5 + \dfrac{2}{9} = \dfrac{{45}}{9} + \dfrac{2}{9} = \dfrac{{47}}{9}\)
Vậy đáp án đúng là \(\dfrac{{47}}{9}\).

Điền số thích hợp vào ô trống:
Một hình chữ nhật có chiều rộng là \(35dm\). Như vậy chiều rộng bằng $\dfrac{5}{7}$ chiều dài.
Vậy diện tích hình chữ nhật đó là
\(cm^2\).
Một hình chữ nhật có chiều rộng là \(35dm\). Như vậy chiều rộng bằng $\dfrac{5}{7}$ chiều dài.
Vậy diện tích hình chữ nhật đó là
\(cm^2\).
- Tính chiều dài hình chữ nhật: theo đề bài ta có $\dfrac{5}{7}$ của chiều dài là \(35dm\), để tính chiều dài ta lấy \(35\) chia cho \(5\) rồi nhân với \(7\), sau đó ghi thêm đơn vị đo vào kết quả.
- Tính diện tích hình chữ nhật theo công thức: Diện tích \(=\) chiều dài \(\times\) chiều rộng.
- Đổi số đo diện tích sang đơn vị đo là xăng-ti-mét vuông.
Chiều dài hình chữ nhật đó là:
\(35:5 \times 7 = 49\,\,(dm)\)
Diện tích hình chữ nhật đó là:
\(\begin{array}{l}49 \times 35 = 1715\left( {d{m^2}} \right)\\1715d{m^2} = 171500c{m^2}\end{array}\)
Đáp số: \(171500c{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(171500\).
Nối kết quả với phép tính tương ứng:
\(\dfrac{5}{6} + \dfrac{5}{8}\)
\(\dfrac{{27}}{{32}} \times \dfrac{4}{9}\)
\(\dfrac{7}{6} - \dfrac{3}{4}\)
\(\dfrac{{25}}{4}:3\)
\(\dfrac{{25}}{{12}}\)
\(\dfrac{3}{8}\)
\(\dfrac{{35}}{{24}}\)
\(\dfrac{5}{{12}}\)
\(\dfrac{5}{6} + \dfrac{5}{8}\)
\(\dfrac{{35}}{{24}}\)
\(\dfrac{{27}}{{32}} \times \dfrac{4}{9}\)
\(\dfrac{3}{8}\)
\(\dfrac{7}{6} - \dfrac{3}{4}\)
\(\dfrac{5}{{12}}\)
\(\dfrac{{25}}{4}:3\)
\(\dfrac{{25}}{{12}}\)
Xem lại quy tắc thực hiện các phép tính cộng, trừ, nhân, chia hai phân số để tính giá trị các phép tính, sau đó nối với kết quả tương ứng.
Ta có:
\(\begin{array}{l}\dfrac{5}{6} + \dfrac{5}{8} = \dfrac{{20}}{{24}} + \dfrac{{15}}{{24}} = \dfrac{{35}}{{24}}\,\,\,\,;\,\,\\\dfrac{{27}}{{32}} \times \dfrac{4}{9} = \dfrac{{27 \times 4}}{{32 \times 9}} = \dfrac{{9 \times 3 \times 4}}{{8 \times 4 \times 9}} = \dfrac{3}{8}\,\,\,;\\\dfrac{7}{6} - \dfrac{3}{4}\, = \dfrac{{14}}{{12}} - \dfrac{9}{{12}} = \dfrac{5}{{12}}\,\,\,\,;\,\,\\\dfrac{{25}}{4}:3 = \,\,\dfrac{{25}}{4}:\dfrac{3}{1} = \,\,\dfrac{{25}}{4} \times \dfrac{1}{3} = \dfrac{{25}}{{12}}\end{array}\)
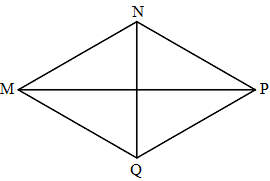
Chọn đáp án đúng hoặc sai cho mỗi khẳng định bên dưới:

Trong hình thoi MNPQ:
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Trong hình thoi MNPQ ta có:
- Hai cặp cạnh đối diện song song: MN song song với PQ, NP song song với MQ.
- Bốn cạnh bằng nhau: MN = NP = PQ = QM.
Vậy các khẳng định đúng là b,c, d; khẳng định sai là a.
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Tổng của hai số là \(765\), nếu giảm số lớn đi \(4\) lần thì ta được số bé.
Vậy hiệu của hai số đó là
Tổng của hai số là \(765\), nếu giảm số lớn đi \(4\) lần thì ta được số bé.
Vậy hiệu của hai số đó là
- Theo đề bài giảm số lớn đi \(4\) lần thì ta được số bé nên tỉ số của số bé và số lớn là \(\dfrac{1}{4}\). Ta biểu diễn số bé bằng \(1\) phần, số lớn bằng \(4\) phần như thế. Ta tìm hai số theo công thức:
Số bé = (Tổng : tổng số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (Tổng : tổng số phần bằng nhau) × số phần của số lớn.
- Tìm hiệu hai số = số lớn - số bé .
Theo đề bài giảm số lớn đi \(4\) lần thì ta được số bé nên tỉ số của số bé và số lớn là \(\dfrac{1}{4}\).
Ta có sơ đồ
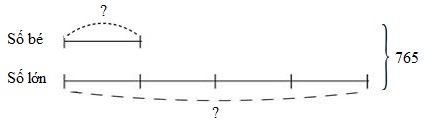
Theo sơ đồ, tổng số phần bằng nhau là:
\(4 + 1 = 5\) (phần)
Số lớn là:
\(765:5 \times 4 = 612\)
Số bé là:
\(765 - 612 = 153\)
Hiệu hai số đó là:
\(612 - 153 = 459\)
Đáp số: \(459\).
Vậy đáp án đúng điền vào ô trống là \(459\).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Một hình chữ nhật có chu vi là \(468cm\). Biết chiều rộng bằng \(\dfrac{5}{8}\) chiều dài.
Vậy diện tích hình chữ nhật đó là
\(c{m^2}\).
Một hình chữ nhật có chu vi là \(468cm\). Biết chiều rộng bằng \(\dfrac{5}{8}\) chiều dài.
Vậy diện tích hình chữ nhật đó là
\(c{m^2}\).
- Tính nửa chu vi = chu vi \(:\,2\), tức là tìm được tổng của chiều dài và chiều rộng. Từ đây ta đưa được về bài toán dạng tìm hai số khi biết tổng và tỉ số của hai số.
Theo bài ra chiều rộng bằng \(\dfrac{5}{8}\) chiều dài nên ta vẽ sơ đồ biểu thị chiều rộng gồm \(5\) phần, chiều dài gồm \(8\) phần như thế. Cọi chiều rộng là số bé, chiều dài là số lớn, ta tìm hai số theo công thức:
Số bé = (tổng : tổng số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (tổng : tổng số phần bằng nhau) × số phần của số lớn.
- Tính diện tích = chiều dài × chiều rộng.
Nửa chu vi hình chữ nhật đó là:
\(468:2 = 234\,(cm)\)
Ta có sơ đồ:
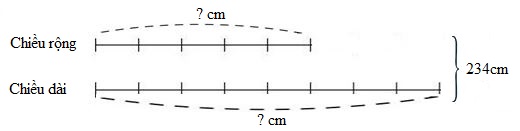
Theo sơ đồ, tổng số phần bằng nhau là:
\(5 + 8 = 13\) (phần)
Chiều rộng hình chữ nhật đó là:
\(234:13 \times 5 = 90\,(cm)\)
Chiều dài hình chữ nhật đó là:
\(234 - 90 = 144\,(cm)\)
Diện tích hình chữ nhật đó là:
\(144 \times 90 = 12960\,\,(c{m^2})\)
Đáp số: \(12960c{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(12960\).
 Tính giá trị biểu thức: \(5 - \dfrac{3}{8}:\dfrac{5}{{12}}\)
Tính giá trị biểu thức: \(5 - \dfrac{3}{8}:\dfrac{5}{{12}}\)
A. \(\dfrac{{111}}{{10}}\)
B. \(\dfrac{{41}}{{10}}\)
C. \(\dfrac{{35}}{{24}}\)
D. \(\dfrac{{155}}{{32}}\)
B. \(\dfrac{{41}}{{10}}\)
Biểu thức có phép cộng và phép chia thì ta thực hiện phép tính chia trước, phép tính cộng sau.
Ta có:
\(5 - \dfrac{3}{8}:\dfrac{5}{{12}} = 5 - \dfrac{3}{8} \times \dfrac{{12}}{5} = 5 - \dfrac{{3 \times 12}}{{8 \times 5}} \)
\(= 5 - \dfrac{{3 \times 4 \times 3}}{{4 \times 2 \times 5}} = 5 - \dfrac{9}{{10}} = \dfrac{{50}}{{10}} - \dfrac{9}{{10}} = \dfrac{{41}}{{10}}\)
Vậy đáp án đúng là \(\dfrac{{41}}{{10}}\).

Điền số thích hợp vào ô trống:
Có \(2\) xe tải lớn, mỗi xe chở được \(4525kg\) gạo và \(3\) xe tải nhỏ, mỗi xe chở được $3600kg$ gạo.
Vậy trung bình mỗi xe tải chở được
\(kg\) gạo.
Có \(2\) xe tải lớn, mỗi xe chở được \(4525kg\) gạo và \(3\) xe tải nhỏ, mỗi xe chở được $3600kg$ gạo.
Vậy trung bình mỗi xe tải chở được
\(kg\) gạo.
- Tìm số gạo \(2\) xe tải lớn chở được.
- Tìm số gạo \(3\) xe tải nhỏ chở được.
- Tìm tổng số gạo \(5\) xe chở được.
- Tìm số gạo trung bình mỗi xe chở được ta lấy tổng số gạo chia cho \(5\).
\(2\) xe tải lớn chở được số ki-lô-gam gạo là:
$4525 \times 2 = 9050\,\,(kg)$
\(3\) xe tải màu nhỏ chở được số ki-lô-gam gạo là:
$3600\,\, \times \,\,3{\rm{ }} = {\rm{ 10800}}\,\,{\rm{(kg)}}$
\(5\) xe tải chở được số ki-lô-gam gạo là:
$9050 + 10800 = 19850\,\,(kg)$
Trung bình mỗi xe tải chở được số ki-lô-gam gạo là:
$19850:5 = 3970\,\,(kg)$
Đáp số: \(3970kg\).
Vậy đáp án đúng điền vào ô trống là \(3970\).

Giá trị của biểu thức \(\dfrac{3}{4} - \dfrac{2}{5} \times \dfrac{7}{8}\) là:
A. \(\dfrac{1}{4}\)
B. \(\dfrac{2}{5}\)
C. \(\dfrac{4}{5}\)
D. \(\dfrac{{49}}{{160}}\)
B. \(\dfrac{2}{5}\)
Biểu thức có phép trừ và phép nhân thì ta thực hiện phép tính nhân trước, phép tính trừ sau.
Ta có:
\(\dfrac{3}{4} - \dfrac{2}{5} \times \dfrac{7}{8} = \dfrac{3}{4} - \dfrac{{2 \times 7}}{{5 \times 8}} = \dfrac{3}{4} - \dfrac{7}{{20}} = \dfrac{{15}}{{20}} - \dfrac{7}{{20}} = \dfrac{8}{{20}} = \dfrac{2}{5}\)
Vậy giá trị của biểu thức \(\dfrac{3}{4} - \dfrac{2}{5} \times \dfrac{7}{8}\) là \(\dfrac{2}{5}\) .

Một mảnh đất hình chữ nhật có chiều dài \(27m\), chiều rộng bằng \(\dfrac{2}{3}\) chiều dài. Người ta sử dụng \(\dfrac{5}{9}\) diện tích để trồng hoa, \(\dfrac{1}{6}\) diện tích để làm đường đi và phần diện tích còn lại để xây bể nước. Tính diện tích phần xây bể nước.
A. \(81{m^2}\)
B. \(486{m^2}\)
C. \(270{m^2}\)
D. \(135{m^2}\)
D. \(135{m^2}\)
- Tìm chiều rộng của mảnh đất, tức là ta tìm \(\dfrac{2}{3}\) của \(27m\).
- Tìm diện tích cả mảnh đất hình chữ nhật ta lấy chiều dài nhân với chiều rộng.
- Tìm diện tích dùng để trồng hoa, tức là ta tìm \(\dfrac{5}{9}\) của diện tích.
- Tìm diện tích dùng để làm đường, tức là ta tìm \(\dfrac{1}{6}\) của diện tích.
- Tìm diện tích dùng để xây bể nước ta lấy diện tích mảnh vườn trừ đi tổng diện tích đất trồng hoa và diện tích để làm đường đi.
Chiều rộng mảnh đất đó là:
\(27 \times \dfrac{2}{3} = 18\,\,(m)\)
Diện tích mảnh đất hình chữ nhật là:
\(27 \times 18 = 486\,\,({m^2})\)
Diện tích trồng hoa là:
\(486\, \times \dfrac{5}{9}\, = 270\,\,({m^2})\)
Diện tích làm đường đi là:
\(486\, \times \dfrac{1}{6}\, = 81\,\,({m^2})\)
Diện tích để xây bể nước là:
\(486\, - (270 + 81) = 135\,\,({m^2})\)
Đáp số: \(135{m^2}\).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Hiệu của hai số là \(882\). Số thứ nhất là số tròn chục và nếu xóa đi chữ số \(0\) ở bên phải số thứ nhất thì được số thứ hai.
Vậy số thứ nhất là
, số thứ hai là
Hiệu của hai số là \(882\). Số thứ nhất là số tròn chục và nếu xóa đi chữ số \(0\) ở bên phải số thứ nhất thì được số thứ hai.
Vậy số thứ nhất là
, số thứ hai là
Bài toán cho biết hiệu của hai số là \(882\). Vì số thứ nhất là số tròn chục và nếu xóa đi chữ số \(0\) ở bên phải số thứ nhất thì được số thứ hai nên số thứ nhất gấp 10 lần số thứ hai. Từ đây ta đưa được về bài toán dạng tìm hai số khi biết hiệu và tỉ số của hai số.
Ta vẽ sơ đồ biểu thị số thứ hai là 1 phần, số thứ nhất là 10 phần như thế. Coi số thứ nhất là số lớn, số thứ hai là số bé, ta tìm hai số theo công thức:
Số bé = (hiệu : hiệu số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (hiệu : hiệu số phần bằng nhau) × số phần của số lớn.
Vì số thứ nhất là số tròn chục và nếu xóa đi chữ số \(0\) ở bên phải số thứ nhất thì được số thứ hai nên số thứ nhất gấp 10 lần số thứ hai.
Ta có sơ đồ:
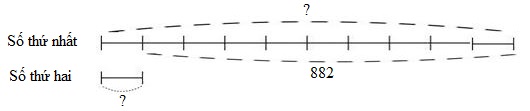
Theo sơ đồ, hiệu số phần bằng nhau là:
\(10 - 1 = 9\) (phần)
Số thứ hai là:
\(882:9 \times 1 = 98\)
Số thứ nhất là:
\(98 \times 10 = 980\)
Đáp số: Số thứ nhất: \(980\);
Số thứ hai: \(98\).
Vậy hai số điền vào ô trống theo thứ tự từ trái qua phải là \(980\,;\,\,98\).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Tổng số học sinh của trường Hoàng Diệu và trường Lê Lợi là \(1275\) học sinh. Nếu chuyển \(54\) học sinh từ trường Hoàng Diệu sang trường Lê Lợi thì trường Lê Lợi có nhiều hơn trường Hoàng Diệu \(35\) học sinh.
Vậy lúc đầu trường Hoàng Diệu có
học sinh,
trường Lê Lợi có
học sinh.
Tổng số học sinh của trường Hoàng Diệu và trường Lê Lợi là \(1275\) học sinh. Nếu chuyển \(54\) học sinh từ trường Hoàng Diệu sang trường Lê Lợi thì trường Lê Lợi có nhiều hơn trường Hoàng Diệu \(35\) học sinh.
Vậy lúc đầu trường Hoàng Diệu có
học sinh,
trường Lê Lợi có
học sinh.
- Nếu chuyển \(54\) học sinh từ trường Hoàng Diệu sang trường Lê Lợi thì tổng số học sinh của hai trường không thay đổi và bằng \(1275\) học sinh.
- Khi đó ta có tổng số học sinh lúc sau của cả hai trường và hiệu số học sinh lúc sau.
- Tìm số học sinh lúc sau của mỗi trường dựa vào công thức tìm hai số khi biết tổng và hiệu của hai số đó:
Số bé = (tổng – hiệu) : $2$ ; Số lớn = (tổng + hiệu) : $2$
- Tìm số học sinh ban đầu:
Số học sinh ban đầu của trường Lê Lợi = số học sinh lúc sau của trường Lê Lợi – \(54\) học sinh.
Số học sinh ban đầu của trường Hoàng Diệu = tổng số học sinh – số học sinh ban đầu của trường Lê Lợi.
Nếu chuyển \(54\) học sinh từ trường Hoàng Diệu sang trường Lê Lợi thì tổng số học sinh của hai trường không thay đổi và bằng \(1275\) học sinh.
Ta có sơ đồ biểu thị số học sinh lúc sau của hai trường:

Lúc sau trường Lê Lợi có số học sinh là:
\((1275 + 35):\,\,2 = 655\) (học sinh)
Lúc đầu trường Lê Lợi có số học sinh là:
\(655 - 54 = 601\) (học sinh)
Lúc đầu trường Hoàng Diệu có số học sinh là:
\(1275 - 601 = 674\) (học sinh)
Đáp số: Trường Hoàng Diệu: \(674\) học sinh;
Trường Lê Lợi: \(601\) học sinh.
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là \(674\,\,;\,\,\,601\).

Điền số thích hợp vào ô trống:
Trong đợt kiểm tra học kì I vừa qua ở lớp 4A thầy giáo nhận thấy \(\dfrac{1}{2}\) số học sinh đạt điểm giỏi, \(\dfrac{2}{5}\) số học sinh đạt điểm khá, \(4\) học sinh đạt điểm trung bình và không có học sinh nào đạt điểm yếu.
Vậy lớp 4A có
học sinh đạt điểm giỏi,
học sinh đạt điểm khá.
Trong đợt kiểm tra học kì I vừa qua ở lớp 4A thầy giáo nhận thấy \(\dfrac{1}{2}\) số học sinh đạt điểm giỏi, \(\dfrac{2}{5}\) số học sinh đạt điểm khá, \(4\) học sinh đạt điểm trung bình và không có học sinh nào đạt điểm yếu.
Vậy lớp 4A có
học sinh đạt điểm giỏi,
học sinh đạt điểm khá.
Muốn biết lớp 4A có bao nhiêu học sinh đạt điểm giỏi, bao nhiêu học sinh đạt điểm khá ta cần cần tính được tổng số học sinh của lớp 4A.
Để giải bài này ta có thể làm như sau:
- Coi học sinh cả lớp là \(1\) đơn vị.
- Tìm phân số chỉ tổng số học sinh giỏi và học sinh khá: \(\dfrac{1}{2} + \dfrac{2}{5} = \dfrac{9}{{10}}\) số học sinh .
- Tìm phân số chỉ số học sinh trung bình ta lấy \(1\) trừ đi phân số chỉ tổng số học sinh giỏi và học sinh khá: \(1 - \dfrac{9}{{10}} = \dfrac{1}{{10}}\) số học sinh.
- Tìm số học sinh cả lớp: theo đề bài ta có \(\dfrac{1}{{10}}\) số học sinh sẽ là \(4\) học sinh, để tính số học sinh cả lớp ta lấy \(4\) chia cho \(1\) rồi nhân với \(10\).
- Tìm số học sinh giỏi ta lấy số học sinh cả lớp nhân với \(\dfrac{1}{2}\).
- Tìm số học sinh khá ta lấy số học sinh cả lớp nhân với \(\dfrac{2}{5}\).
Coi học sinh cả lớp là \(1\) đơn vị.
Số học sinh giỏi và học sinh khá chiếm số phần học sinh cả lớp là:
\(\dfrac{1}{2} + \dfrac{2}{5} = \dfrac{9}{{10}}\) (số học sinh)
Số học sinh trung bình chiếm số phần học sinh cả lớp là:
\(1 - \dfrac{9}{{10}} = \dfrac{1}{{10}}\) (số học sinh)
Lớp 4A có số học sinh là:
\(4:1 \times 10 = 40\) (học sinh)
Lớp 4A có số học sinh giỏi là:
\(40 \times \dfrac{1}{2} = 20\) (học sinh)
Lớp 4A có số học sinh là:
\(40 \times \dfrac{2}{5} = 16\) (học sinh)
Đáp số: Học sinh giỏi: \(20\) học sinh;
Học sinh khá: \(16\) học sinh.
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là \(20\,;\,\,16\).

Có thể viết được bao nhiêu phân số từ ba chữ số \(2\,;\,\,4\,;\,\,7\), trong đó tử số và mẫu số là các số có một chữ số và tử số khác mẫu số?
A. \(6\) số
B. \(7\) số
C. \(8\) số
D. \(9\) số
A. \(6\) số
Từ các số đã cho ta có thể viết được các phân số mà tử số khác mẫu số đó là:
\(\dfrac{2}{4}\,;\,\,\dfrac{4}{2}\,;\,\,\dfrac{2}{7}\,;\,\,\dfrac{7}{2}\,;\,\,\dfrac{4}{7}\,;\,\,\dfrac{7}{4}\)
Vậy có \(6\) phân số thoả mãn yêu cầu đề bài.
 Điền số thích hợp vào ô trống :
Điền số thích hợp vào ô trống :
Sân trường của trường tiểu học Kim Đồng dạng hình chữ nhật có chiều dài \(75m\), chiều rộng \(45m\) được vẽ trên bản đồ tỉ lệ \(1:1500\).
Vậy trên bản đồ, chu vi của sân trường đó là
\(cm\).
Sân trường của trường tiểu học Kim Đồng dạng hình chữ nhật có chiều dài \(75m\), chiều rộng \(45m\) được vẽ trên bản đồ tỉ lệ \(1:1500\).
Vậy trên bản đồ, chu vi của sân trường đó là
\(cm\).
- Đổi số đo chiều dài và chiều rộng sang đơn vị đo là xăng-ti-mét.
- Tính số đo chiều dài trên bản đồ ta lấy chiều dài thực tế (với đơn vị đo là xăng-ti-mét) chia cho \(1500\).
- Tính số đo chiều rộng trên bản đồ ta lấy chiều rộng thực tế (với đơn vị đo là xăng-ti-mét) chia cho \(1500\).
- Tính chu vi sân trường trên bản đồ ta lấy tổng chiều dài và chiều rộng trên bản đồ nhân với \(2\).
Ta có: \(75m = 7500cm;\,\,\,\,\,\,\,\,\,45m = 4500cm\)
Chiều dài của sân trường trên bản đồ dài số xăng-ti-mét là:
\(7500:1500 = 5\,\,(cm)\)
Chiều rộng của sân trường trên bản đồ dài số xăng-ti-mét là:
\(4500:1500 = 3\,\,(cm)\)
Chu vi của sân trường trên bản đồ dài số xăng-ti-mét là:
\((5 + 3) \times 2 = 16\,\,(cm)\)
Đáp số: \(16cm\).
Vậy đáp án đúng điền vào ô trống là \(16\).