Đề thi học kì 2 - Đề số 1
Đề bài

Điền số thích hợp vào ô trống:
Tổng của hai số là số chẵn nhỏ nhất có bốn chữ số khác nhau. Biết số lớn gấp \(3\) lần số bé.
Vậy số lớn là
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
\(37245 + 53432 = \,\)

Thực hiện tính:

Điền số thích hợp vào ô trống:
Lớp 4A có \(14\) học sinh nữ. Số học sinh nữ chiếm \(\dfrac{2}{5}\) số học sinh của cả lớp.
Vậy lớp 4A có tất cả
học sinh.

Điền số thích hợp vào ô trống:
Viết phân số sau dưới dạng thương:

Số \(975\,\,386\) được đọc là:
A. Chín mươi bảy nghìn năm nghìn ba trăm tám mươi sáu
B. Chín trăm bảy lăm nghìn ba trăm tám sáu
C. Chín trăm bảy mươi lăm triệu ba trăm tám sáu
D. Chín trăm bảy mươi lăm nghìn ba trăm tám mươi sáu
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
\(4\) tạ \( = \)
yến
Biểu đồ dưới đây nói về các môn thể thao khối lớp Bốn tham gia:
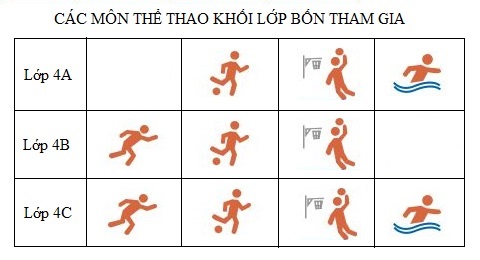
Hỏi lớp 4A tham gia mấy môn thể thao, gồm những môn nào?
A. \(4\) môn, đó là chạy, bóng đá, bóng chuyền, bơi
B. \(3\) môn, đó là bóng đá, bóng rổ, bơi.
C. \(3\) môn, đó là chạy, bóng đá, bóng rổ.
D. \(2\) môn, đó là chạy, bóng rổ.

Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là:
A. \(\dfrac{2}{5}\)
B. \(\dfrac{3}{5}\)
C. \(\dfrac{{18}}{{45}}\)
D. \(\dfrac{8}{{20}}\)

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{3}{5} \cdot \cdot \cdot \dfrac{5}{6}\)
A. \( < \)
B. \( > \)
C. \( = \)

Chọn phân số bé hơn trong hai phân số sau:
A. \(\dfrac{{198}}{{199}}\)
B. \(\dfrac{{1998}}{{1999}}\)

Chọn dấu thích hợp điền vào ô trống:
\(\dfrac{3}{4} \times \dfrac{8}{{15}} + \dfrac{1}{3}\,\,\,\,\cdot \cdot \cdot \,\,\,\,2 - \dfrac{2}{5} \times 3\)
A. \( < \)
B. \( > \)
C. \( = \)

Lớp 4B có \(18\) học sinh nữ. Số học sinh nam bằng \(\dfrac{8}{9}\) số học sinh nữ. Hỏi lớp 4B có tất cả bao nhiêu học sinh?
A. \(16\) học sinh
B. \(32\) học sinh
C. \(34\) học sinh
D. \(36\) học sinh

Tìm \(y\), biết: \(y \times \dfrac{3}{8} = 2 + \dfrac{{10}}{7}\)
A. \(y = \dfrac{9}{{14}}\)
B. \(y = \dfrac{9}{7}\)
C. \(y = \dfrac{{32}}{7}\)
D. \(y = \dfrac{{64}}{7}\)

Một hộp đựng \(7\) quả bóng xanh và \(9\) quả bóng đỏ. Tỉ số của số quả bóng đỏ và số quả bóng xanh là:
A. \(\dfrac{7}{{16}}\)
B. \(\dfrac{9}{{16}}\)
C. \(\dfrac{7}{9}\)
D. \(\dfrac{9}{7}\)

Một thoi có độ dài đường chéo lớn hơn độ dài đường chéo bé là \(51cm\). Tính diện tích hình thoi đó, biết rằng tỉ số giữa độ dài đường chéo lớn và độ dài đường chéo bé là \(\dfrac{7}{4}\) .
A. \(4046c{m^2}\)
B. \(4064c{m^2}\)
C. \(8092c{m^2}\)
D. \(8128c{m^2}\)

Điền số thích hợp vào ô trống:
Trên bản đồ tỉ lệ \(1:200\), chiều dài một căn phòng đo được \(5cm\).
Vậy chiều dài thật của căn phòng đó là
\(m\).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Một trường tiểu học có ít hơn \(235\) học sinh và nhiều hơn \(215\) học sinh. Nếu học sinh trong trường xếp thành \(3\) hàng hoặc \(5\) hàng thì không thừa, không thiếu bạn nào.
Vậy trường tiểu học đó có tất cả
học sinh.
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Có \(3\) đội trồng rừng, trung bình mỗi đội trồng được \(428\) cây xanh. Đội một trồng được $375$ cây, đội hai trồng được nhiều hơn đội một \(56\) cây.
Vậy đội ba trồng được
cây.

Điền số thích hợp vào ô trống:
Khối lớp \(3\) có \(135\) học sinh. Khối lớp \(4\) có số học sinh bằng \(\dfrac{6}{5}\) số học sinh khối lớp \(3\).
Vậy hai khối có tất cả
học sinh.
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Hình thoi ABCD có độ dài đường chéo AC là \(40cm\), độ dài đường chéo BD bằng \(\dfrac{3}{5}\) độ dài đường chéo AC. Hình chữ nhật GHIK có chiều rộng là \(15cm\) và diện tích bằng diện tích hình thoi ABCD.
Vậy chu vi hình chữ nhật GHIK là
\(cm\).

Tổng của \(2\) số là số lớn nhất có \(4\) chữ số, hiệu của \(2\) số là số lẻ nhỏ nhất có \(3\) chữ số khác nhau. Vậy hai số đó là:
A. \(5152\) và \(4847\)
B. \(5051\) và \(4948\)
C. \(5150\) và \(4849\)
D. \(5049\) và \(4951\)
 Một trang trại nuôi \(323\) con trâu và bò, sau đó người ta bán đi \(25\) con bò và \(18\) con trâu thì số con trâu còn lại bằng \(\dfrac{3}{5}\) số con bò còn lại. Hỏi trước khi bán số con bò của trang trại nhiều hơn số con trâu bao nhiêu con?
Một trang trại nuôi \(323\) con trâu và bò, sau đó người ta bán đi \(25\) con bò và \(18\) con trâu thì số con trâu còn lại bằng \(\dfrac{3}{5}\) số con bò còn lại. Hỏi trước khi bán số con bò của trang trại nhiều hơn số con trâu bao nhiêu con?
A. \(80\) con
B. \(77\) con
C. \(74\) con
D. \(70\) con

Điền số thích hợp vào ô trống:
Trước đây \(5\) năm tổng số tuổi hiện nay của hai bà cháu là \(62\) tuổi. Hiện nay tuổi bà gấp \(7\) lần tuổi cháu.
Vậy hiện nay bà
tuổi, cháu
tuổi.

Một quầy lương thực buổi sáng bán được \(\dfrac{2}{7}\) tổng số gạo, buổi chiều bán được nhiều hơn buổi sáng \(\dfrac{1}{5}\) tổng số gạo. Hỏi số gạo còn lại chiếm bao nhiêu phần số gạo của quầy lương thực đó?
A. \(\dfrac{4}{{35}}\) tổng số gạo
B. \(\dfrac{8}{{35}}\) tổng số gạo
C. \(\dfrac{{27}}{{35}}\) tổng số gạo
D. \(\dfrac{{17}}{{35}}\) tổng số gạo
 Một người có \(4\) tạ gạo tẻ và gạo nếp. Sau khi người đó bán đi \(72kg\) gạo tẻ và \(23kg\) gạo nếp thì còn lại số gạo nếp bằng \(\dfrac{1}{4}\) số gạo tẻ. Hỏi lúc đầu người đó có bao nhiêu ki-lô-gam gạo mỗi loại?
Một người có \(4\) tạ gạo tẻ và gạo nếp. Sau khi người đó bán đi \(72kg\) gạo tẻ và \(23kg\) gạo nếp thì còn lại số gạo nếp bằng \(\dfrac{1}{4}\) số gạo tẻ. Hỏi lúc đầu người đó có bao nhiêu ki-lô-gam gạo mỗi loại?
A. \(320kg\) gạo tẻ; \(80kg\) gạo nếp
B. \(316kg\) gạo tẻ; \(84kg\) gạo nếp
C. \(325kg\) gạo tẻ; \(75kg\) gạo nếp
D. \(339kg\) gạo tẻ; \(61kg\) gạo nếp

Hiện nay mẹ hơn con \(25\) tuổi. Cách đây \(3\) năm tuổi con bằng \(\dfrac{1}{6}\) tuổi mẹ. Tính tuổi của mỗi người hiện nay.
A. Con \(7\) tuổi; mẹ \(32\) tuổi
B. Con \(9\) tuổi; mẹ \(34\) tuổi
C. Con \(8\) tuổi; mẹ \(33\) tuổi
D. Con \(11\) tuổi; mẹ \(36\) tuổi
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Tuổi trung bình của các cầu thủ đội bóng chuyền (có \(6\) người) là \(21\) tuổi. Nếu không tính đội trưởng thì tuổi trung bình của \(5\) cầu thủ còn lại là \(20\) tuổi.
Vậy tuổi của đội trưởng là
tuổi.

Có bao nhiêu phân số bằng phân số \(\dfrac{{12}}{{18}}\) sao cho mẫu số nhỏ hơn \(30\)?
A. \(5\) phân số
B. \(6\) phân số
C. \(7\) phân số
D. \(8\) phân số

Tính bằng cách thuận tiện:
Lời giải và đáp án

Điền số thích hợp vào ô trống:
Tổng của hai số là số chẵn nhỏ nhất có bốn chữ số khác nhau. Biết số lớn gấp \(3\) lần số bé.
Vậy số lớn là
Tổng của hai số là số chẵn nhỏ nhất có bốn chữ số khác nhau. Biết số lớn gấp \(3\) lần số bé.
Vậy số lớn là
- Tìm số chẵn nhỏ nhất có bốn chữ số khác nhau là \(1024\). Vậy tổng của hai số là \(1024\). Khi đó ta có bài toán tìm hai số khi biết tổng và tỉ số.
- Theo đề bài số lớn gấp \(3\) lần số bé nên ta vẽ sơ đồ biểu thị số bé gồm \(1\) phần, số lớn gồm \(3\) phần như thế. Ta tìm số lớn theo công thức:
Số lớn = (Tổng : tổng số phần bằng nhau) × số phần của số lớn.
Số chẵn nhỏ nhất có bốn chữ số khác nhau là \(1024\). Vậy tổng của hai số là \(1024\).
Ta có sơ đồ:
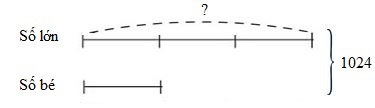
Theo sơ đồ, tổng số phần bằng nhau là:
\(1 + 3 = 4\) (phần)
Số lớn là:
\(1024:4 \times 3 = 768\)
Đáp số: \(768\).
Vậy đáp án đúng điền vào ô trống là \(768\).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
\(37245 + 53432 = \,\)
\(37245 + 53432 = \,\)
Muốn cộng hai số tự nhiên ta có thể làm như sau:
- Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
- Cộng các chữ số ở từng hàng theo thứ tự từ phải sang trái, tức là từ hàng đơn vị đến hàng chục, hàng trăm, hàng nghìn, … .
Ta đặt tính và thực hiện tính như sau:
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{37245}\\{53432}\end{array}}\\\hline{\,\,\,\,90677}\end{array}\)
Vậy \(37245 + 53432 = \,90677\) Đáp án đúng điền vào ô trống là \(90677\).

Thực hiện tính:
Áp dụng quy tắc trừ hai phân số có cùng mẫu số: Muốn trừ hai phân số có cùng mẫu số, ta trừ tử số của phân số thứ nhất cho mẫu số của phân số thứ hai và giữ nguyên mẫu số.
Ta có: \(\dfrac{{19}}{{25}} - \dfrac{7}{{25}} = \dfrac{{19 - 7}}{{25}} = \dfrac{{12}}{{25}}\)
Vậy đáp án đúng điền vào chỗ chấm lần lượt từ trên xuống dưới là \(12\,;\,\,25\).

Điền số thích hợp vào ô trống:
Lớp 4A có \(14\) học sinh nữ. Số học sinh nữ chiếm \(\dfrac{2}{5}\) số học sinh của cả lớp.
Vậy lớp 4A có tất cả
học sinh.
Lớp 4A có \(14\) học sinh nữ. Số học sinh nữ chiếm \(\dfrac{2}{5}\) số học sinh của cả lớp.
Vậy lớp 4A có tất cả
học sinh.
Theo đề bài ta có \(\dfrac{2}{5}\) số học sinh của cả lớp là \(14\) học sinh. Để tìm số học sinh của lớp ta có thể lấy \(14\) chia cho \(2\) rồi nhân với \(5\) hoặc lấy \(14\) chia cho \(\dfrac{2}{5}\), sau đó thêm đơn vị vào kết quả.
Lớp 4A có tất cả số học sinh là:
\(14:2 \times 5 = 35\) (học sinh)
Đáp số: \(35\) học sinh.
Vậy đáp án đúng điền vào ô trống là \(35\).

Điền số thích hợp vào ô trống:
Viết phân số sau dưới dạng thương:
Tử số chính là số bị chia, mẫu số là số chia.
Muốn tìm thương ta lấy số bị chia chia cho số chia, hay ta lấy tử số chia cho mẫu số.
Ta có: \( \dfrac{{24}}{{49}}=24:49\).
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là \(24\,;\,\,49\).

Số \(975\,\,386\) được đọc là:
A. Chín mươi bảy nghìn năm nghìn ba trăm tám mươi sáu
B. Chín trăm bảy lăm nghìn ba trăm tám sáu
C. Chín trăm bảy mươi lăm triệu ba trăm tám sáu
D. Chín trăm bảy mươi lăm nghìn ba trăm tám mươi sáu
D. Chín trăm bảy mươi lăm nghìn ba trăm tám mươi sáu
Khi đọc số ta đọc từ trái sang phải, hay từ hàng cao tới hàng thấp.
Số \(975\,\,386\) được đọc là chín trăm bảy mươi lăm nghìn ba trăm tám mươi sáu.
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
\(4\) tạ \( = \)
yến
\(4\) tạ \( = \)
yến
Dựa vào bảng đơn vị đo khối lượng và nhận xét mỗi đơn vị đo khối lượng đều gấp \(10\) lần đơn vị bé hơn, liền nó, ta có \(1\) tạ $ = {\rm{ }}10$ yến.
Ta có: \(1\) tạ $ = {\rm{ }}10$ yến nên \(4\) tạ $ = 10$ yến $ \times \,\,4 = \,\,40$ yến. Vậy đáp án đúng điền vào ô trống là \(40\).
Biểu đồ dưới đây nói về các môn thể thao khối lớp Bốn tham gia:

Hỏi lớp 4A tham gia mấy môn thể thao, gồm những môn nào?
A. \(4\) môn, đó là chạy, bóng đá, bóng chuyền, bơi
B. \(3\) môn, đó là bóng đá, bóng rổ, bơi.
C. \(3\) môn, đó là chạy, bóng đá, bóng rổ.
D. \(2\) môn, đó là chạy, bóng rổ.
B. \(3\) môn, đó là bóng đá, bóng rổ, bơi.
Quan sát biểu đồ, hàng thứ nhất chỉ các môn thể thao lớp 4A tham gia.
Nhìn vào biểu đồ ta thấy lớp 4A tham gia \(3\) môn thể thao, đó là bóng đá, bóng rổ, bơi.

Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là:
A. \(\dfrac{2}{5}\)
B. \(\dfrac{3}{5}\)
C. \(\dfrac{{18}}{{45}}\)
D. \(\dfrac{8}{{20}}\)
A. \(\dfrac{2}{5}\)
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\).
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Ta thấy phân số \(\dfrac{{72}}{{180}}\) có tử số và mẫu số đều chia hết cho \(4\), nên ta có:
\(\dfrac{{72}}{{180}} = \dfrac{{72:4}}{{180:4}} = \dfrac{{18}}{{45}}\)
Ta thấy phân số \(\dfrac{{18}}{{45}}\) có tử số và mẫu số đều chia hết cho \(9\), nên ta có:
\(\dfrac{{18}}{{45}} = \dfrac{{18:9}}{{45:9}} = \dfrac{2}{5}\)
Ta thấy phân số \(\dfrac{2}{5}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{2}{5}\) là phân số tối giản.
Vậy \(\dfrac{{72}}{{180}} = \dfrac{2}{5}\).

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{3}{5} \cdot \cdot \cdot \dfrac{5}{6}\)
A. \( < \)
B. \( > \)
C. \( = \)
A. \( < \)
Quy đồng mẫu số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
\(MSC = 30\).
Quy đồng mẫu số hai phân số ta có:
\(\dfrac{3}{5} = \dfrac{{3 \times 6}}{{5 \times 6}} = \dfrac{{18}}{{30}};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{5}{6} = \dfrac{{5 \times 5}}{{6 \times 5}} = \dfrac{{25}}{{30}}\)
Mà \(\dfrac{{18}}{{30}} < \dfrac{{25}}{{30}}\) (vì \(18 < 25\)).
Vậy \(\dfrac{3}{5} < \dfrac{5}{6}\).

Chọn phân số bé hơn trong hai phân số sau:
A. \(\dfrac{{198}}{{199}}\)
B. \(\dfrac{{1998}}{{1999}}\)
A. \(\dfrac{{198}}{{199}}\)
Phần bù của \(\dfrac{{198}}{{199}}\) là \(\dfrac{1}{{199}}\).
Phần bù của \(\dfrac{{1998}}{{1999}}\) là \(\dfrac{1}{{1999}}\).
Mà \(\dfrac{1}{{199}} > \dfrac{1}{{1999}}\) (vì \(199 < 1999\)).
Do đó \(\dfrac{{198}}{{199}} < \dfrac{{1998}}{{1999}}\).
Vậy phân số bé hơn là \(\dfrac{{198}}{{199}}\).

Chọn dấu thích hợp điền vào ô trống:
\(\dfrac{3}{4} \times \dfrac{8}{{15}} + \dfrac{1}{3}\,\,\,\,\cdot \cdot \cdot \,\,\,\,2 - \dfrac{2}{5} \times 3\)
A. \( < \)
B. \( > \)
C. \( = \)
A. \( < \)
Tính giá trị biểu thức ở hai vế rồi so sánh kết quả với nhau.
Biểu thức có chứa phép cộng, trừ, nhân, chia thì ta thực hiện phép nhân, phép chia trước, phép cộng và phép trừ sau.
Ta có:
+) $\dfrac{3}{4} \times \dfrac{8}{{15}} + \dfrac{1}{3} = \dfrac{2}{5} + \dfrac{1}{3} = \,\dfrac{{11}}{{15}}$ ;
+) $2 - \dfrac{2}{5} \times 3\, = \,2 - \dfrac{6}{5} = \,\dfrac{4}{5} = \dfrac{{12}}{{15}}\,$
Mà \(\dfrac{{11}}{{15}} < \dfrac{{12}}{{15}}\), hay \(\dfrac{{11}}{{15}} < \dfrac{4}{5}\).
Do đó \(\dfrac{3}{4} \times \dfrac{8}{{15}} + \dfrac{1}{3}\,\,\, < \,\,\,2 - \dfrac{2}{5} \times 3\).
Vậy dấu thích hợp điền vào ô trống là \( < \).

Lớp 4B có \(18\) học sinh nữ. Số học sinh nam bằng \(\dfrac{8}{9}\) số học sinh nữ. Hỏi lớp 4B có tất cả bao nhiêu học sinh?
A. \(16\) học sinh
B. \(32\) học sinh
C. \(34\) học sinh
D. \(36\) học sinh
C. \(34\) học sinh
- Tìm số học sinh nam, tức là ta đi tìm \(\dfrac{8}{9}\) của \(18\) học sinh.
- Số học sinh cả lớp bằng tổng của học sinh nam và học sinh nữ.
Lớp 4B có số học sinh nam là:
\(18 \times \dfrac{8}{9} = 16\) (học sinh)
Lớp 4B có tất cả số học sinh là:
\(18 + 16 = 34\) (học sinh)
Đáp số: \(34\) học sinh.

Tìm \(y\), biết: \(y \times \dfrac{3}{8} = 2 + \dfrac{{10}}{7}\)
A. \(y = \dfrac{9}{{14}}\)
B. \(y = \dfrac{9}{7}\)
C. \(y = \dfrac{{32}}{7}\)
D. \(y = \dfrac{{64}}{7}\)
D. \(y = \dfrac{{64}}{7}\)
- Tính giá trị vế phải.
- \(y\) ở vị trí thừa số chưa biết, muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
Ta có:
\(\begin{array}{l}y \times \dfrac{3}{8} = 2 + \dfrac{{10}}{7}\\y \times \dfrac{3}{8} = \dfrac{{14}}{7} + \dfrac{{10}}{7}\\y \times \dfrac{3}{8} = \dfrac{{24}}{7}\\y = \dfrac{{24}}{7}:\dfrac{3}{8}\\y = \dfrac{{64}}{7}\end{array}\)
Vậy đáp án đúng là \(y = \dfrac{{64}}{7}\).

Một hộp đựng \(7\) quả bóng xanh và \(9\) quả bóng đỏ. Tỉ số của số quả bóng đỏ và số quả bóng xanh là:
A. \(\dfrac{7}{{16}}\)
B. \(\dfrac{9}{{16}}\)
C. \(\dfrac{7}{9}\)
D. \(\dfrac{9}{7}\)
D. \(\dfrac{9}{7}\)
Áp dụng định nghĩa : Tỉ số của \(a\) và \(b\) là \(a:b\) hay \(\dfrac{a}{b}\) (\(b\) khác \(0\)).
Có \(7\) quả bóng xanh và \(9\) quả bóng đỏ nên tỉ số của số quả bóng đỏ và số quả bóng xanh là \(\dfrac{9}{7}\).

Một thoi có độ dài đường chéo lớn hơn độ dài đường chéo bé là \(51cm\). Tính diện tích hình thoi đó, biết rằng tỉ số giữa độ dài đường chéo lớn và độ dài đường chéo bé là \(\dfrac{7}{4}\) .
A. \(4046c{m^2}\)
B. \(4064c{m^2}\)
C. \(8092c{m^2}\)
D. \(8128c{m^2}\)
A. \(4046c{m^2}\)
- Theo bài ra tỉ số giữa độ dài đường chéo lớn và độ dài đường chéo bé là \(\dfrac{7}{4}\) nên ta vẽ sơ đồ biểu thị đường chéo bé gồm \(4\) phần, đường chéo lớn gồm \(7\) phần như thế. Cọi đường chéo bé là số bé, đường chéo lớn là số lớn, ta tìm hai số theo công thức:
Số bé = (hiệu : hiệu số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (hiệu : hiệu số phần bằng nhau) × số phần của số lớn.
- Tính diện tích hình thoi ta lấy tích độ dài hai đường chéo chia cho \(2\).
Ta có sơ đồ:
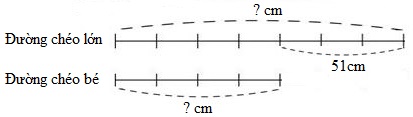
Theo sơ đồ, hiệu số phần bằng nhau là:
\(7 - 4 = 3\) (phần)
Độ dài đường chéo lớn là:
\(51:3 \times 7 = 119\,(cm)\)
Độ dài đường chéo bé là:
\(119 - 51 = 68\,(cm)\)
Diện tích hình thoi đó là:
\(119 \times 68:2 = 4046\,(c{m^2})\)
Đáp số: \(4046c{m^2}\).

Điền số thích hợp vào ô trống:
Trên bản đồ tỉ lệ \(1:200\), chiều dài một căn phòng đo được \(5cm\).
Vậy chiều dài thật của căn phòng đó là
\(m\).
Trên bản đồ tỉ lệ \(1:200\), chiều dài một căn phòng đo được \(5cm\).
Vậy chiều dài thật của căn phòng đó là
\(m\).
- Tìm độ dài thật ta lấy độ dài thu nhỏ nhân với độ dài thật ứng với \(1cm\) trên bản đồ.
- Đổi đơn vị đo vừa tìm được sang đơn vị đo là mét.
Chiều dài thật của căn phòng đó là:
\(\begin{array}{l}5 \times 200 = 1000\,\,(cm)\\1000cm = 10m\end{array}\)
Đáp số: \(10m\)
Vậy đáp án đúng điền vào ô trống là \(10\).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Một trường tiểu học có ít hơn \(235\) học sinh và nhiều hơn \(215\) học sinh. Nếu học sinh trong trường xếp thành \(3\) hàng hoặc \(5\) hàng thì không thừa, không thiếu bạn nào.
Vậy trường tiểu học đó có tất cả
học sinh.
Một trường tiểu học có ít hơn \(235\) học sinh và nhiều hơn \(215\) học sinh. Nếu học sinh trong trường xếp thành \(3\) hàng hoặc \(5\) hàng thì không thừa, không thiếu bạn nào.
Vậy trường tiểu học đó có tất cả
học sinh.
- Tìm số học sinh có thể có dựa vào điều kiện ít hơn \(235\) học sinh và nhiều hơn \(215\) học sinh.
- Áp dụng dấu hiệu chia hết cho \(3\) và \(5\).
Vì số học sinh ít hơn \(235\) học sinh và nhiều hơn \(215\) học sinh nên số học sinh có thể là \(216\,;\,\,217\,;\,\,218\,;\,\,...\,\,;\,\,233\,;\,\,234\).
Vì học sinh trong trường xếp thành \(3\) hàng hoặc \(5\) hàng thì không thừa, không thiếu bạn nào nên số học sinh của trường đó là số chia hết cho cả \(3\) và \(5\).
Số học sinh là số chia hết cho \(5\) nên ta chỉ xét các số \(220\,;\,\,225\,;\,\,230\).
Số \(220\) có tổng các chữ số là: \(2 + 2 + 0 = 4\).
Vì \(4\) không chia hết cho \(3\) nên số \(220\) không chia hết cho \(3\) (loại).
Số \(225\) có tổng các chữ số là: \(2 + 2 + 5 = 9\).
Vì \(9\) chia hết cho \(3\) nên số \(225\) chia hết cho \(3\) (chọn).
Số \(230\) có tổng các chữ số là: \(2 + 3 + 0 = 5\).
Vì \(5\) không chia hết cho \(3\) nên số \(230\) không chia hết cho \(3\) (loại).
Vậy trường đó có tất cả \(225\) học sinh.
Đáp án đúng điền vào ô trống là \(225\).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Có \(3\) đội trồng rừng, trung bình mỗi đội trồng được \(428\) cây xanh. Đội một trồng được $375$ cây, đội hai trồng được nhiều hơn đội một \(56\) cây.
Vậy đội ba trồng được
cây.
Có \(3\) đội trồng rừng, trung bình mỗi đội trồng được \(428\) cây xanh. Đội một trồng được $375$ cây, đội hai trồng được nhiều hơn đội một \(56\) cây.
Vậy đội ba trồng được
cây.
- Tính tổng số cây ba đội trồng được ta lấy số trung bình cộng nhân với \(3\).
- Tính số cây đội hai trồng ta lấy số cây đội một trồng được cộng với \(56\) cây.
- Tính số cây đội ba trồng ta lấy tổng số cây ba đội trồng trừ đi tổng số cây đội một và đội hai trồng.
Cả ba đội trồng được số cây là:
\(428 \times 3 = 1284\) (cây)
Đội hai trồng được số cây là:
\(375 + 56 = 431\) (cây)
Đội ba trồng được số cây là:
\(1284 - (375 + 431) = 478\) (cây)
Đáp số: \(478\) cây.
Vậy đáp án đúng điền vào ô trống là \(478\).

Điền số thích hợp vào ô trống:
Khối lớp \(3\) có \(135\) học sinh. Khối lớp \(4\) có số học sinh bằng \(\dfrac{6}{5}\) số học sinh khối lớp \(3\).
Vậy hai khối có tất cả
học sinh.
Khối lớp \(3\) có \(135\) học sinh. Khối lớp \(4\) có số học sinh bằng \(\dfrac{6}{5}\) số học sinh khối lớp \(3\).
Vậy hai khối có tất cả
học sinh.
- Tìm số học sinh khối lớp \(4\) ta lấy số học sinh khối lớp \(3\) nhân với \(\dfrac{6}{5}\).
- Số học sinh của cả hai khối = số học sinh khối lớp \(3\) + số học sinh khối lớp \(4\).
Khối lớp \(4\) có số học sinh là:
\(135 \times \dfrac{6}{5} = 162\) (học sinh)
Hai khối có tất cả học sinh là:
\(135 + 162 = 297\) (học sinh)
Đáp số: \(297\) học sinh.
Vậy đáp án đúng điền vào ô trống là \(297\).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Hình thoi ABCD có độ dài đường chéo AC là \(40cm\), độ dài đường chéo BD bằng \(\dfrac{3}{5}\) độ dài đường chéo AC. Hình chữ nhật GHIK có chiều rộng là \(15cm\) và diện tích bằng diện tích hình thoi ABCD.
Vậy chu vi hình chữ nhật GHIK là
\(cm\).
Hình thoi ABCD có độ dài đường chéo AC là \(40cm\), độ dài đường chéo BD bằng \(\dfrac{3}{5}\) độ dài đường chéo AC. Hình chữ nhật GHIK có chiều rộng là \(15cm\) và diện tích bằng diện tích hình thoi ABCD.
Vậy chu vi hình chữ nhật GHIK là
\(cm\).
- Tính độ dài đường chéo BD ta lấy độ dài đường chéo AC nhân với \(\dfrac{3}{5}\).
- Tính diện tích hình thoi ABCD ta lấy tích độ dài đường chéo AC và đường chéo BD chia cho \(2\).
- Tính chiều dài hình chữ nhật ta lấy diện tích chia cho chiều rộng.
- Tính chu vi hình chữ nhật ta lấy tổng của chiều dài và chiều rộng rồi nhân với \(2\).
Độ dài đường chéo BD là:
\(40 \times \dfrac{3}{5} = 24\,\,(cm)\)
Diện tích hình thoi ABCD là:
\(40 \times 24\,:2 = 480\,\,(c{m^2})\)
Vì hình chữ nhật GHIK có diện tích bằng diện tích hình thoi ABCD nên diện tích hình chữ nhật GHIK là \(480c{m^2}\).
Chiều dài hình chữ nhật là:
\(480:15 = 32\,\,(cm)\)
Chu vi hình chữ nhật là:
\((32 + 15) \times 2 = 94\,\,(cm)\)
Đáp số: \(94cm\).
Vậy đáp án đúng điền vào ô trống là \(94\).

Tổng của \(2\) số là số lớn nhất có \(4\) chữ số, hiệu của \(2\) số là số lẻ nhỏ nhất có \(3\) chữ số khác nhau. Vậy hai số đó là:
A. \(5152\) và \(4847\)
B. \(5051\) và \(4948\)
C. \(5150\) và \(4849\)
D. \(5049\) và \(4951\)
B. \(5051\) và \(4948\)
- Tìm số lớn nhất có \(4\) chữ số và số lẻ nhỏ nhất có \(3\) chữ số khác nhau.
- Áp dụng công thức tìm hai số khi biết tổng và hiệu của hai số đó:
Số bé = (tổng – hiệu) : $2$ ; Số lớn = (tổng + hiệu) : $2$
Số lớn nhất có 4 chữ số là $9999$. Do đó tổng của \(2\) số đó là $9999$.
Số lẻ nhỏ nhất có \(3\) chữ số khác nhau là $103$. Do đó hiệu của \(2\) số đó là $103$.
Ta có sơ đồ:
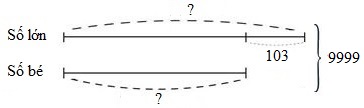
Số bé là:
$(9999 - 103):2 = 4948$
Số lớn là:
$4948 + 103 = 5051$
Đáp số: Số lớn: \(5051\); số bé: \(4948\).
 Một trang trại nuôi \(323\) con trâu và bò, sau đó người ta bán đi \(25\) con bò và \(18\) con trâu thì số con trâu còn lại bằng \(\dfrac{3}{5}\) số con bò còn lại. Hỏi trước khi bán số con bò của trang trại nhiều hơn số con trâu bao nhiêu con?
Một trang trại nuôi \(323\) con trâu và bò, sau đó người ta bán đi \(25\) con bò và \(18\) con trâu thì số con trâu còn lại bằng \(\dfrac{3}{5}\) số con bò còn lại. Hỏi trước khi bán số con bò của trang trại nhiều hơn số con trâu bao nhiêu con?
A. \(80\) con
B. \(77\) con
C. \(74\) con
D. \(70\) con
B. \(77\) con
- Đề bài cho tổng số trâu bò ban đầu nhưng lại cho tỉ số giữa trâu và bò sau khi bán đi một số con. Để tính được lúc đầu số con bò của trang trại nhiều hơn số con trâu bao nhiêu con , ta sẽ đi tìm xem sau khi bán thì mỗi loại còn lại bao nhiêu con.
- Tìm tổng số con trâu và bò còn lại sau khi bán đi \(25\) con bò và \(18\) con trâu:
\(323 - 25 - 18 = 280\) (con)
Từ đây ta đưa được về bài toán dạng tìm hai số khi biết tổng và tỉ số của hai số.
Theo đề bài, số con trâu còn lại bằng \(\dfrac{3}{5}\) số con bò còn lại nên ta vẽ sơ đồ biểu thị số con trâu còn lại là \(3\) phần, số con bò còn lại là \(5\) phần như thế. Coi số con bò còn lại là số lớn, số con trâu còn lại là số bé, ta tìm hai số theo công thức:
Số bé = (tổng : tổng số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (tổng : tổng số phần bằng nhau) × số phần của số lớn.
- Tìm số trâu lúc đầu = số trâu còn lại sau khi bán + \(18\) con.
Số bò lúc đầu = tổng số trâu bò lúc đầu – số trâu lúc đầu.
- Hiệu giữa số bò và số trâu lúc ban đầu = số bò lúc đầu – số trâu lúc đầu.
Sau khi bán, tổng số con trâu và con bò còn lại là:
\(323 - 25 - 18 = 280\) (con)
Ta có sơ đồ biểu thị số trâu, bò còn lại sau khi bán:
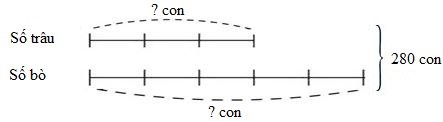
Theo sơ đồ, tổng số phần bằng nhau là:
\(3 + 5 = 8\) (phần)
Số con trâu còn lại là:
$280:8 \times 3 = 105$ (con)
Lúc đầu nông trại có số con trâu là:
$105 + 18 = 123$ (con)
Lúc đầu nông trại có số con bò là:
$323 - 123 = 200$ (con)
Trước khi bán số con bò của trang trại nhiều hơn số con trâu số con là:
$200 - 123 = 77$ (con)
Đáp số: \(77\) con.

Điền số thích hợp vào ô trống:
Trước đây \(5\) năm tổng số tuổi hiện nay của hai bà cháu là \(62\) tuổi. Hiện nay tuổi bà gấp \(7\) lần tuổi cháu.
Vậy hiện nay bà
tuổi, cháu
tuổi.
Trước đây \(5\) năm tổng số tuổi hiện nay của hai bà cháu là \(62\) tuổi. Hiện nay tuổi bà gấp \(7\) lần tuổi cháu.
Vậy hiện nay bà
tuổi, cháu
tuổi.
- Tìm số tuổi của mỗi người hiện nay, ta dựa vào tổng số tuổi của hai bà cháu trước đây \(5\) năm và tỉ số về số tuổi của hai bà cháu hiện nay.
- Vì mỗi năm mỗi người tăng thêm 1 tuổi và tổng số tuổi của hai bà cháu trước đây \(5\) năm là \(62\) tuổi nên tổng số tuổi của hai bà cháu hiện nay là \(62 + 5 + 5 = 72\) tuổi. Từ đây ta đưa được về bài toán dạng tìm hai số khi biết tổng và tỉ số của hai số. Ta vẽ sơ đồ biểu diễn tuổi cháu hiện nay là \(1\) phần, tuổi bà hiện nay là \(7\) phần. Coi số tuổi của cháu là số bé, số tuổi của bà là số lớn, ta tìm hai số theo công thức:
Số bé = (Tổng : tổng số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (Tổng : tổng số phần bằng nhau) × số phần của số lớn.
Tổng số tuổi của hai bà cháu hiện nay là
\(62 + 5 + 5 = 72\) (tuổi)
Ta có sơ đồ tuổi của hai bà cháu hiện nay:
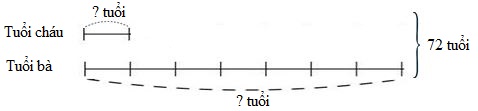
Theo sơ đồ, tổng số phần bằng nhau là:
\(7 + 1 = 8\) (phần)
Tuổi cháu hiện nay là:
\(72:8 \times 1 = 9\) (tuổi)
Tuổi bà hiện nay là:
\(9 \times 7 = 63\,\) (tuổi)
Đáp số: Bà: \(63\) tuổi;
Cháu: \(9\) tuổi
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là \(63\,;\,\,9\).

Một quầy lương thực buổi sáng bán được \(\dfrac{2}{7}\) tổng số gạo, buổi chiều bán được nhiều hơn buổi sáng \(\dfrac{1}{5}\) tổng số gạo. Hỏi số gạo còn lại chiếm bao nhiêu phần số gạo của quầy lương thực đó?
A. \(\dfrac{4}{{35}}\) tổng số gạo
B. \(\dfrac{8}{{35}}\) tổng số gạo
C. \(\dfrac{{27}}{{35}}\) tổng số gạo
D. \(\dfrac{{17}}{{35}}\) tổng số gạo
B. \(\dfrac{8}{{35}}\) tổng số gạo
- Coi tổng số gạo là \(1\) đơn vị.
- Tìm số gạo bán trong buổi chiều ta lấy số gạo bán được trong buổi sáng cộng với \(\dfrac{1}{5}\).
- Tìm tổng số gạo đã bán trong hai buổi sáng và chiều.
- Tìm số gạo còn lại ta lấy \(1\) trừ đi tổng số gạo đã bán trong hai buổi sáng và chiều.
Trong buổi chiều, quầy lương thực đó đã bán được số gạo là:
\(\dfrac{2}{7} + \dfrac{1}{5} = \dfrac{{17}}{{35}}\) (tổng số gạo)
Trong buổi sáng và buổi chiều, quầy lương thực đó đã bán được số gạo là:
\(\dfrac{2}{7} + \dfrac{{17}}{{35}} = \dfrac{{27}}{{35}}\) (tổng số gạo)
Số gạo còn lại của quầy lương thực đó là:
\(1 - \dfrac{{27}}{{35}} = \dfrac{8}{{35}}\) (tổng số gạo)
Đáp số: \(\dfrac{8}{{35}}\) tổng số gạo.
 Một người có \(4\) tạ gạo tẻ và gạo nếp. Sau khi người đó bán đi \(72kg\) gạo tẻ và \(23kg\) gạo nếp thì còn lại số gạo nếp bằng \(\dfrac{1}{4}\) số gạo tẻ. Hỏi lúc đầu người đó có bao nhiêu ki-lô-gam gạo mỗi loại?
Một người có \(4\) tạ gạo tẻ và gạo nếp. Sau khi người đó bán đi \(72kg\) gạo tẻ và \(23kg\) gạo nếp thì còn lại số gạo nếp bằng \(\dfrac{1}{4}\) số gạo tẻ. Hỏi lúc đầu người đó có bao nhiêu ki-lô-gam gạo mỗi loại?
A. \(320kg\) gạo tẻ; \(80kg\) gạo nếp
B. \(316kg\) gạo tẻ; \(84kg\) gạo nếp
C. \(325kg\) gạo tẻ; \(75kg\) gạo nếp
D. \(339kg\) gạo tẻ; \(61kg\) gạo nếp
B. \(316kg\) gạo tẻ; \(84kg\) gạo nếp
- Đề bài cho tổng số gạo ban đầu nhưng lại cho tỉ số giữa gạo nếp và gạo tẻ lúc sau. Để tính được lúc đầu người ta có bao nhiêu ki-lô-gam gạo mỗi loại, ta sẽ đi tìm xem sau khi bán thì mỗi loại còn lại bao nhiêu ki-lô-gam gạo.
- Đổi \(4\) tạ = \(400kg\) gạo,
Tìm số gạo còn lại bán đi \(72kg\) gạo tẻ và \(23kg\) gạo nếp là \(400 - 72 - 23 = 305kg\).
Từ đây ta đưa được về bài toán dạng tìm hai số khi biết tổng và tỉ số của hai số.
Theo bài ra số gạo nếp còn lại bằng \(\dfrac{1}{4}\) số gạo tẻ nên ta vẽ sơ đồ biểu thị số gạo nếp gồm \(1\) phần, số gạo tẻ gồm \(4\) phần như thế. Cọi số gạo nếp là số bé, số gạo tẻ là số lớn, ta tìm hai số theo công thức:
Số bé = (Tổng : tổng số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (Tổng : tổng số phần bằng nhau) × số phần của số lớn
- Số gạo tẻ lúc đầu = số gạo tẻ lúc sau + \(72kg\).
Số gạo nếp lúc đầu = tổng số gạo lúc đầu – số gạo tẻ lúc đầu.
Đổi \(4\) tạ \( = 400kg\)
Sau khi bán, người đó còn lại số ki-lô-gam gạo tẻ và gạo nếp là:
\(400 - 72 - 23 = 305\,\,(kg)\)
Ta có sơ đồ biểu diễn số gạo còn lại sau khi bán:

Theo sơ đồ, tổng số phần bằng nhau là:
\(4 + 1 = 5\) (phần)
Số gạo nếp còn lại sau khi bán là:
\(305:5 = 61\,(kg)\)
Ban đầu người đó có số ki-lô-gam gạo nếp là:
\(61 + 23 = 84\,(kg)\)
Ban đầu người đó có số ki-lô-gam gạo tẻ là:
\(400 - 84 = 316\,(kg)\)
Đáp số: \(316kg\) gạo tẻ; \(84kg\) gạo nếp.

Hiện nay mẹ hơn con \(25\) tuổi. Cách đây \(3\) năm tuổi con bằng \(\dfrac{1}{6}\) tuổi mẹ. Tính tuổi của mỗi người hiện nay.
A. Con \(7\) tuổi; mẹ \(32\) tuổi
B. Con \(9\) tuổi; mẹ \(34\) tuổi
C. Con \(8\) tuổi; mẹ \(33\) tuổi
D. Con \(11\) tuổi; mẹ \(36\) tuổi
C. Con \(8\) tuổi; mẹ \(33\) tuổi
- Vì mỗi năm mỗi người tăng thêm 1 tuổi nên hiệu số tuổi không thay đổi. Hiện nay mẹ hơn con \(25\) tuổi thì cách đây \(3\) năm, mẹ vẫn hơn con \(25\) tuổi . Từ đây ta đưa được về bài toán dạng tìm hai số khi biết hiệu và tỉ số của hai số. Ta vẽ sơ đồ biểu diễn tuổi con cách đây \(3\) năm là \(1\) phần, tuổi mẹ cách đây \(3\) năm là \(6\) phần. Coi số tuổi của con là số bé, số tuổi của mẹ là số lớn, ta tìm hai số theo công thức:
Số bé = (Hiệu : hiệu số phần bằng nhau)× số phần của số bé
hoặc
Số lớn = (Hiệu : hiệu số phần bằng nhau)× số phần của số lớn.
- Tìm số tuổi hiện nay của mỗi người ta lấy số tuổi cách đây \(3\) năm cộng thêm \(3\) tuổi.
Vì mỗi năm mỗi người tăng thêm 1 tuổi nên hiệu số tuổi không thay đổi. Hiện nay mẹ hơn con \(25\) tuổi thì cách đây \(3\) năm, mẹ vẫn hơn con \(25\) tuổi .
Ta có sơ đồ tuổi của hai mẹ con cách đây \(3\) năm:
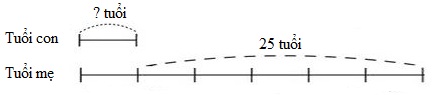
Theo sơ đồ, hiệu số phần bằng nhau là:
\(6 - 1 = 5\) (phần)
Tuổi con cách đây \(3\) năm là:
\(25:5 \times 1 = 5\) (tuổi)
Tuổi con hiện nay là:
\(5 + 3 = 8\) (tuổi)
Tuổi mẹ hiện nay là:
\(8 + 25 = 33\) (tuổi)
Đáp số: Con \(8\) tuổi; mẹ \(33\) tuổi.
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Tuổi trung bình của các cầu thủ đội bóng chuyền (có \(6\) người) là \(21\) tuổi. Nếu không tính đội trưởng thì tuổi trung bình của \(5\) cầu thủ còn lại là \(20\) tuổi.
Vậy tuổi của đội trưởng là
tuổi.
Tuổi trung bình của các cầu thủ đội bóng chuyền (có \(6\) người) là \(21\) tuổi. Nếu không tính đội trưởng thì tuổi trung bình của \(5\) cầu thủ còn lại là \(20\) tuổi.
Vậy tuổi của đội trưởng là
tuổi.
- Tính tổng số tuổi của $6$ cầu thủ; tổng số tuổi của \(5\) cầu thủ theo công thức:
Tổng = trung bình cộng \( \times \) số các số hạng
- Tính tuổi của đội trưởng ta lấy tổng số tuổi của $6$ cầu thủ trừ đi tổng số tuổi của \(5\) cầu thủ.
Tổng số tuổi của các cầu thủ đội bóng chuyền là:
\(21 \times 6 = 126\) (tuổi)
Tổng số tuổi của \(5\) cầu thủ là:
\(20 \times 5 = 100\) (tuổi)
Tuổi của đội trưởng là:
\(126 - 100 = 26\) (tuổi)
Đáp số: \(26\) tuổi.
Vậy đáp án đúng điền vào ô trống là \(26\).

Có bao nhiêu phân số bằng phân số \(\dfrac{{12}}{{18}}\) sao cho mẫu số nhỏ hơn \(30\)?
A. \(5\) phân số
B. \(6\) phân số
C. \(7\) phân số
D. \(8\) phân số
D. \(8\) phân số
- Nhận xét $18 \times 2 = 36\,,\,\;\left( {36 > 30} \right)\;$ (không thoả mãn điều kiện mẫu số nhỏ hơn \(30\)) nên ta sẽ không nhân cả tử số và mẫu số của phân số \(\dfrac{{12}}{{18}}\) với cùng số tự nhiên nào lớn hơn \(1\).
- Rút gọn phân số \(\dfrac{{12}}{{18}}\) thành phân số tối giản rồi tìm các phân số bằng phân số đó và có mẫu số nhỏ hơn \(30\).
Vì phân số đã cho có mẫu số là \(18\) và $18 \times 2 = 36\,,\,\,\;\left( {36 > 30} \right)\;$(không thoả mãn điều kiện mẫu số nhỏ hơn \(30\)) nên ta sẽ không nhân cả tử số và mẫu số của phân số \(\dfrac{{12}}{{18}}\) với cùng số tự nhiên nào lớn hơn \(1\).
Rút gọn phân số \(\dfrac{{12}}{{18}}\) ta có: \(\dfrac{{12}}{{18}} = \dfrac{{12:6}}{{18:6}} = \dfrac{2}{3}\).
Ta sẽ tìm các phân số bằng phân số \(\dfrac{2}{3}\) và có mẫu số nhỏ hơn \(30\).
$\begin{array}{l}\dfrac{2}{3} = \dfrac{{2 \times 2}}{{3 \times 2}} = \dfrac{4}{6}\,\,\,;\, \quad \quad \quad \quad \quad \, \dfrac{2}{3} = \dfrac{{2 \times 3}}{{3 \times 3}} = \dfrac{6}{9}\\\dfrac{2}{3} = \dfrac{{2 \times 4}}{{3 \times 4}} = \dfrac{8}{{12}}\,\,\,;\,\,\,\quad \quad \quad \quad \; \dfrac{2}{3} = \dfrac{{2 \times 5}}{{3 \times 5}} = \dfrac{{10}}{{15}}\\\dfrac{2}{3} = \dfrac{{2 \times 6}}{{3 \times 6}} = \dfrac{{12}}{{18}}\,\,\,;\,\,\quad \quad \quad \quad \quad \dfrac{2}{3} = \dfrac{{2 \times 7}}{{3 \times 7}} = \dfrac{{14}}{{21}}\\\dfrac{2}{3} = \dfrac{{2 \times 8}}{{3 \times 8}} = \dfrac{{16}}{{24}}\,\,\,;\,\,\quad \quad \quad \quad \quad \dfrac{2}{3} = \dfrac{{2 \times 9}}{{3 \times 9}} = \dfrac{{18}}{{27}}\,\, \cdot \end{array}$
Vậy có \(8\) phân số bằng với phân số \(\dfrac{{12}}{{18}}\) mà mẫu số nhỏ hơn \(30\) là:
$\dfrac{2}{3}\,\,\,;\,\,\,\,\dfrac{4}{6}\,\,\,;\,\,\,\,\dfrac{6}{9}\,\,\,;\,\,\dfrac{8}{{12}}\,\,\,;\,\,\,\,\dfrac{{10}}{{15}}\,\,\,;\,\,\,\,\dfrac{{14}}{{21}}\,\,\,;\,\,\,\,\dfrac{{16}}{{24}}\,\,\,;\,\,\,\,\dfrac{{18}}{{27}}\,\, \cdot $

Tính bằng cách thuận tiện:
Rút gọn các phân số rồi thực hiện nhóm các phân số có cùng mẫu số thành một nhóm.
$\begin{array}{l}\dfrac{4}{5} + \dfrac{2}{{10}} - \dfrac{1}{3} - \dfrac{{10}}{{15}} \\ = \dfrac{4}{5} + \dfrac{1}{5} - \dfrac{1}{3} - \dfrac{2}{3}\\= \left( {\dfrac{4}{5} + \dfrac{1}{5}} \right) - \left( {\dfrac{1}{3} + \dfrac{2}{3}} \right)\\ = \dfrac{5}{5} - \dfrac{3}{3}\\ = \,\,1 - 1 \\= \quad 0\end{array}$