Đề số 5 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán lớp 4
Tải vềĐáp án và lời giải chi tiết Đề số 5 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán lớp 4
Đề bài
Phần I. Trắc nghiệm (3 điểm)
Khoanh vào chữ cái đặt trước câu trả lời đúng nhất
Câu 1. Số nào trong các số dưới đây có chữ số 9 biểu thị cho 9000 ?
A. 29 687 B. 93 574
C. 80 296 D. 17 932
Câu 2. Tích của \(\dfrac{5}{9}\) và \(\dfrac{{10}}{3}\) là :
A. \(\dfrac{{15}}{{90}}\) B. \(\dfrac{{50}}{{27}}\)
C. \(\dfrac{{50}}{9}\) D. \(\dfrac{{90}}{{15}}\)
Câu 3. 5dm 2 6cm 2 = ………… cm 2 . Số thích hợp điền vào chỗ chấm là :
A. 56 B. 506
C. 560 D. 5600
Câu 4. Một hình thoi có độ dài hai đường chéo lần lượt là 40dm và 2m. Diện tích của hình thoi đó là :
A. 800dm 2 B. 80dm 2
C. 800dm D. 400dm 2
Câu 5. Số trung bình cộng của: 36, 38 và 40 là :
A. 35 B. 36
C. 38 D. 39
Câu 6. Mẹ hơn con 28 tuổi. Tuổi mẹ gấp 5 lần tuổi con. Tính tuổi của mỗi người.
A. Mẹ: 37 tuổi ; con : 9 tuổi B. Mẹ: 30 tuổi ; con : 6 tuổi
C. Mẹ: 40 tuổi ; con : 8 tuổi D. Mẹ: 35 tuổi ; con : 7 tuổi
Phần II. Tự luận
Bài 1. (2 điểm) Tính
\(a) \;\dfrac{9}{{10}} + \dfrac{3}{8}\) \(b) \;\dfrac{7}{4} - \dfrac{3}{5}\)
\(c)\,\,\dfrac{4}{3} \times \dfrac{9}{5}\) \(d) \;\dfrac{4}{5}:\dfrac{7}{{10}}\)
Bài 2. ( 1 điểm) Tìm \(y\):
\(a)\,\,\dfrac{5}{7} \times y = \dfrac{2}{3}\) \(b)\,\,\dfrac{2}{9} + y = 1 + \dfrac{2}{3}\)
Bài 3 (3 điểm): Một thửa ruộng hình chữ nhật có nửa chu vi là 175m, chiều rộng bằng \(\dfrac{3}{4}\) chiều dài.
a) Tính diện tích thửa ruộng đó.
b) Người ta trồng lúa trên thửa ruộng đó, cứ 100m 2 thu hoạch được 50kg thóc. Hỏi thửa ruộng đó người ta thu hoạch được bao nhiêu ki-lô-gam thóc?
Bài 4 (1 điểm): Tính bằng cách thuận tiện
a) 486 × 45 + 486 × 55
b) \(\dfrac{{1919}}{{2323}} \times \dfrac{{464646}}{{747474}} \times \dfrac{{37}}{{19}}\)
Lời giải chi tiết
Phần I.
Câu 1.
Phương pháp:
Chữ số 9 biểu thị cho 9000 thì phải thuộc hàng nghìn, ta tìm số có chữ số 9 thuộc hàng nghìn.
Cách giải:
Trong các số đã cho, có chữ số 9 biểu thị cho 9000 là 29 687.
Chọn A.
Câu 2.
Phương pháp:
Muốn tìm tích của hai phân số \(\dfrac{5}{9}\) và \(\dfrac{{10}}{3}\) ta thực hiện phép nhân hai phân số \(\dfrac{5}{9}\)và \(\dfrac{{10}}{3}\).
Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
Cách giải:
Tích của \(\dfrac{5}{9}\) và \(\dfrac{{10}}{3}\) là : \(\dfrac{5}{9} \times \dfrac{{10}}{3} = \dfrac{{5 \times 10}}{{9 \times 3}} = \dfrac{{50}}{{27}}\).
Chọn B.
Câu 3.
Phương pháp:
Áp dụng kiến thức : 1dm 2 = 100cm 2 .
Cách giải:
Ta có 1dm 2 = 100cm 2 nên 5dm 2 = 500cm 2 .
Do đó 5dm 2 6cm 2 = 5dm 2 + 6cm 2 = 500cm 2 + 6cm 2 = 506cm 2 .
Chọn B.
Câu 4.
Phương pháp:
Đổi các số đo về cùng đơn vị đo là đề-xi-mét.
Tính diện tích hình thoi ta lấy tích độ dài hai đường chéo chia cho 2.
Cách giải:
Đổi: 2m = 20dm.
Diện tích của hình thoi đó là :
40 × 20 : 2 = 400 (dm 2 )
Đáp số: 400dm 2 .
Chọn D.
Câu 5.
Phương pháp:
Muốn tìm số trung bình cộng của ba số 36, 38 và 40 ta lấy tổng của ba số chia cho 3.
Cách giải:
Số trung bình cộng của: 36, 38 và 40 là:
(36 + 38 + 40) : 3 = 38
Chọn C.
Câu 6.
Phương pháp:
1. Vẽ sơ đồ: Coi tuổi con gồm 1 phần thì tuổi mẹ gồm 5 phần như thế.
2. Tìm hiệu số phần bằng nhau.
3. Tìm giá trị của một phần bằng cách lấy hiệu chia cho hiệu số phần bằng nhau.
4. Tìm tuổi con (lấy giá trị 1 phần nhân với 1)
5. Tìm tuổi mẹ (lấy tuổi con cộng với 28 tuổi)
Lưu ý: Bước 3 và bước 4 có thể giải gộp thanh 1 bước.
Cách giải:
Ta có sơ đồ:
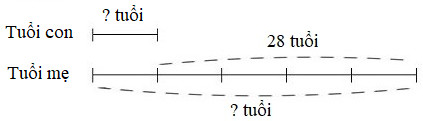
Theo sơ đồ, hiệu số phần bằng nhau là :
5 – 1 = 4 (phần)
Giá trị của một phần là :
28 : 4 = 7 (tuổi)
Tuổi con là :
7 × 1 = 7 (tuổi)\(\)
Tuổi mẹ là :
7 + 28 = 35 (tuổi)
Đáp số : Tuổi con : 7 tuổi;
Tuổi mẹ : 35 tuổi.
Chọn D.
Phần II.
Bài 1.
Phương pháp:
- Muốn cộng hoặc trừ hai phân số ta quy đồng mẫu số hai phân số rồi cộng hoặc trừ hai phân số đó.
- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Cách giải:
a) \(\dfrac{9}{{10}} + \dfrac{3}{8}\)\(=\dfrac{{36}}{{40}} + \dfrac{{15}}{{40}} = \dfrac{{36 + 15}}{{40}} \)\(= \dfrac{{51}}{{40}}\)
b) \(\dfrac{7}{4} - \dfrac{3}{5}\)\( = \dfrac{{35}}{{20}} - \dfrac{{12}}{{20}} = \dfrac{{35 - 12}}{{20}} \)\(= \dfrac{{23}}{{20}}\)
c) \(\dfrac{4}{3} \times \dfrac{9}{5}\)= \(\dfrac{{4 \times 9}}{{3 \times 5}} = \dfrac{{36}}{{15}} = \dfrac{{12}}{5}\)
d) \(\dfrac{4}{5}:\dfrac{7}{{10}} = \dfrac{4}{5} \times \dfrac{{10}}{7} = \dfrac{{4 \times 10}}{{5 \times 7}}\)\( = \dfrac{{40}}{{35}} = \dfrac{8}{7}\)
Bài 2.
Phương pháp:
Áp dụng các quy tắc:
- Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
- Muốn tìm số hạng ta lấy tổng trừ đi số hạng đã biết.
Cách giải:
\(\begin{array}{l}a)\,\,\dfrac{5}{7} \times y = \dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,y = \dfrac{2}{3}:\dfrac{5}{7}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,y = \dfrac{{14}}{{15}}\end{array}\)
\(\begin{array}{l}b)\,\,\dfrac{2}{9} + y = 1 + \dfrac{2}{3}\\\,\,\,\,\,\,\dfrac{2}{9} + y = \dfrac{5}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,y = \dfrac{5}{3} - \dfrac{2}{9}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,y = \dfrac{{13}}{9}\end{array}\)
Bài 3.
Phương pháp:
- Vẽ sơ đồ và tìm chiều dài, chiều rộng theo bài toán tìm hai số khi biết tổng và tỉ số của hai số đó.
- Tính diện tích thửa ruộng ta lấy chiều dài nhân với chiều rộng.
- Tính số thóc thu được ta lấy diện tích thửa ruộng chia cho 100 rồi nhân với 50.
Cách giải:
a) Ta có sơ đồ:
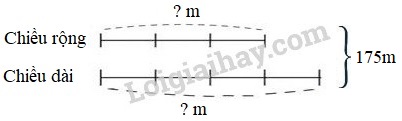
Theo sơ đồ, tổng số phần bằng nhau là :
3 + 4 = 7 (phần)
Chiều rộng thửa ruộng đó là :
175 : 7 × 3 = 75 (m)
Chiều dài thửa ruộng đó là :
25 × 4 = 100 (m)
Diện tích thửa ruộng đó là :
100 × 75 = 7500 (m 2 )
b) Trên thửa ruộng đó người ta thu hoạch được số ki-lô-gam thóc là :
7500 : 100 × 75 = 3750 (kg)
Đáp số: a) 7500m 2 ;
b) 3750kg.
Bài 4 .
Phương pháp:
a) Áp dụng công thức: \(a \times b + a \times c = a \times (b + c)\).
b) Để nhân các phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số. Sau đó phân tích tử số và mẫu số thành tích của các thừa số rồi rút gọn các thừa số giống nhau cho nhau.
Cách giải:
a) 486 × 45 + 486 × 55
= 486 × (45 + 55)
= 486 × 100 = 48600
\(b)\,\,\dfrac{{1919}}{{2323}} \times \dfrac{{464646}}{{747474}} \times \dfrac{{37}}{{19}}\)
\(\begin{array}{l} = \dfrac{{19}}{{23}} \times \dfrac{{46}}{{74}} \times \dfrac{{37}}{{19}}\\ = \dfrac{{19 \times 46 \times 37}}{{23 \times 74 \times 19}}\\ = \dfrac{{19 \times 23 \times 2 \times 37}}{{23 \times 37 \times 2 \times 19}} = 1\end{array}\)