Đề số 8 - Đề kiểm tra học kì 1 - Toán lớp 4
Tải vềĐáp án và lời giải chi tiết Đề số 8 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán lớp 4
Đề bài
I. PHẦN TRẮC NGHIỆM
Khoanh vào chữ đặt trước câu trả lời đúng :
Câu 1. Giá trị của chữ số 5 trong số bé nhất có 6 chữ số khác nhau là :
A. 5 B. 50
C. 500 D. 5000
Câu 2. Viết số thích hợp vào chỗ chấm : 300 yến = …… tấn
A. 3 B. 30
C. 3000 D. 30000
Câu 3. Viết số thích hợp vào chỗ chấm:
4m 2 15dm 2 = …... dm 2
A. 40015 B. 4150
C. 4015 D. 415
Câu 4: Trung bình cộng của hai số là 123. Số bé là 58 thì số lớn là:
A. 65 B. 75
C. 115 D. 188
Câu 5: Hình bên có:

A. 1 góc nhọn, 1 góc tù và 2 góc vuông.
B. 1 góc nhọn, 2 góc tù và 2 góc vuông.
C. 2 góc nhọn, 1 góc tù và 2 góc vuông.
D. 1 góc nhọn, 1 góc tù và 3 góc vuông.
Câu 6. Trong các số dưới đây số nào chia hết cho 5?
A. 70963 B. 90411
C. 65940 D. 55948
II. PHẦN TỰ LUẬN
Bài 1. Đặt tính rồi tính:
386154 + 260765 ;
126 485 – 52 936 ;
308 × 263 ;
25176 : 35.
Bài 2. Tìm \(x\):
a) \(x\) × 74 = 18944
b) \(x\) + 246572 = 1584 × 278
Bài 3. Một mảnh đất hình chữ nhật có chu vi là 144m, chiều rộng kém chiều dài 24m. Tính diện tích mảnh đất hình chữ nhật đó.
Bài 4. Tính giá trị của biểu thức \(a + 567 × b\), với \(a\) là số bé nhất có ba chữ số khác nhau và \(b\) là số lớn nhất có hai chữ số.
Lời giải
I. PHẦN TRẮC NGHIỆM
Câu 1.
Phương pháp:
Viết số bé nhất có 6 chữ số khác nhau rồi xác định hàng của chữ số 5, sau đó viết giá trị của chữ số 5.
Cách giải:
Số bé nhất có 6 chữ số khác nhau là 102 345.
Trong số 102 345, chữ số 5 thuộc hàng đơn vị nên có giá trị là 5.
Chọn A.
Câu 2.
Phương pháp:
Dựa vào bảng đơn vị đo khối lượng:
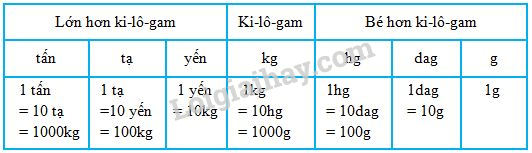
Cách giải:
Ta có: 1 tấn = 100 yến.
Nhẩm: 300 : 100 = 3.
Vậy: 300 yến = 3 tấn.
Chọn A.
Câu 3.
Phương pháp:
Áp dụng cách chuyển đổi: 1 m 2 = 100dm 2 .
Cách giải:
Ta có: 1m 2 = 100dm 2 nên 4m 2 = 400dm 2 .
Do đó: 4m 2 15dm 2 = 4m 2 + 15dm 2 = 400dm 2 + 15dm 2 = 415dm 2 .
Vậy: 4m 2 15dm 2 = 415dm 2 .
Chọn D.
Câu 4.
Phương pháp:
- Tìm tổng của 2 số = số trung bình cộng × 2.
- Tìm số lớn = tổng của 2 số – số bé.
Cách giải:
Tổng của hai số đó là:
123 × 2 = 246
Số lớn là:
246 - 58 = 188
Đáp số: 188.
Chọn D.
Câu 5.
Phương pháp:
Quan sát hình vẽ và dựa vào đặc điểm của các góc để xác định góc vuông, góc nhọn, góc tù, góc bẹt có trong mỗi hình.
Cách giải:
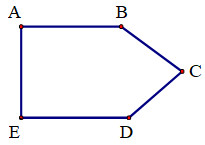
Các góc có trong hình là :
+ Góc vuông đỉnh A; cạnh AB, AE.
+ Góc vuông đỉnh E, cạnh EA, ED.
+ Góc nhọn đỉnh C; cạnh CB, CD.
+ Góc tù đỉnh B, cạnh BA, BC.
+ Góc tù đỉnh D, cạnh DC, DE.
Vậy hình đã cho có 1 góc nhọn, 2 góc tù và 2 góc vuông.
Chọn B.
Câu 6.
Phương pháp:
Áp dụng dấu hiệu chia hết cho 5: Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5.
Cách giải:
Trong các số đã cho, số chia hết cho 5 là 65940 (vì có chữ số tận cùng là 0).
Chọn C.
II. PHẦN TỰ LUẬN
Bài 1.
Phương pháp:
- Đặt tính : Viết các chữ số cùng hàng đặt thẳng cột với nhau.
- Tính : Cộng, trừ hoặc nhân lần lượt từ phải sang trái.
Phép chia ta đặt theo cột dọc, sau đó chia lần lượt từ trái sang phải.
Cách giải:
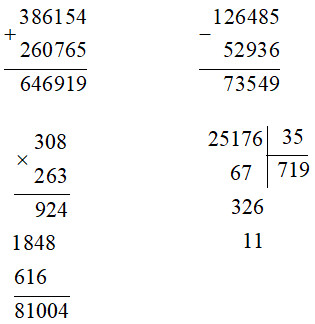
Bài 2.
Phương pháp:
Áp dụng các quy tắc:
- Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
- Muốn tìm số hang chưa biết ta lấy tổng trừ đi số hạng đã biết.
Cách giải:
a) \(x\) × 74 = 18944
\(x\) = 18944 : 74
\(x\) = 256
b) \(x\) + 246572 = 1584 × 278
\(x\) + 246572 = 440352
\(x\) = 440352 – 246572
\(x\) = 193780
Bài 3.
Phương pháp:
- Tính nửa chu vi = chu vi : 2.
- Tìm chiều rộng theo công thức tìm số bé khi biết tổng và hiệu của hai số:
Số bé = (Tổng – Hiệu) : 2
- Tìm chiều dài = nửa chu vi – chiều rộng.
- Tính diện tích = chiều dài × chiều rộng.
(hoặc có thể tìm chiều dài theo công thức tìm số lớn khi biết tổng và hiệu của hai số, sau đó tìm số bé bằng cách lấy nửa chu vi trừ đi chiều dài).
Cách giải:
Nửa chu vi mảnh đất đó là:
144 : 2 = 72 (m)
Chiều rộng của mảnh đất là:
(72 – 24) : 2 = 24 (m)
Chiều dài của mảnh đất là:
72 – 24 = 48 (m)
Diện tích của mảnh đất là:
48 × 24 = 1152 (m 2 )
Đáp số: 1152m 2 .
Bài 4.
Phương pháp:
- Tìm số bé nhất có ba chữ số khác nhau và số lớn nhất có hai chữ số, từ đó ta tìm được giá trị của \(a\) và \(b\).
- Thay giá trị của \(a\) và \(b\) vào biểu thức \(a + 567 × b\) rồi tính giá trị biểu thức đó.
- Biểu thức có phép nhân và phép cộng thì thực hiện phép nhân trước, thực hiện phép cộng sau.
Cách giải:
Số bé nhất có ba chữ số khác nhau là 102. Vậy \(a\) = 102.
Số lớn nhất có hai chữ số là 99. Vậy \(b\) = 99.
Thay \(a\) = 102 và \(b\) = 99 vào biểu thức \(a + 567 × b\) ta được:
102 + 567 × 99
= 102 + 56133
= 56235