Đề số 7 - Đề kiểm tra học kì 1 - Toán 9 — Không quảng cáo

Đề bài

Bài 1: (2 điểm)

a) Tính chu vi tam giác ABC biết độ dài 3 cạnh là \(AB = 5\sqrt 2 \left( {cm} \right),AC = \sqrt {32} \left( {cm} \right)\),\(BC = \sqrt {98} \left( {cm} \right)\). (Không yêu cầu vẽ hình)

b) Thu gọn: \(B = \sqrt {{{\left( {\sqrt 7  - 1} \right)}^2}}  - \dfrac{6}{{\sqrt 7  - 1}}\).

Bài 2: (3,0 điểm) Cho đường thẳng \(\left( {{d_1}} \right):y =  - 3x + 1\) và đường thẳng \(\left( {{d_2}} \right):y = x - 3\).

a)Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng mặt phẳng tọa độ \(Oxy\).

b)Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng phép tính.

c)Tìm \(m\) để đường thẳng \(\left( D \right):y = \left( {2m + 3} \right)x - 5\) song song vơi đường thẳng \(\left( {{d_1}} \right)\).

Bài 3: (1 điểm) Trong một tòa nhà ngoài thang máy người ta còn xây thêm một cầu thang đi bộ. Từ tầng 1 đến tầng 2 có 30 bậc thang. Các tầng còn lại cứ hai tầng liên tiếp cách nhau 21 bậc thang. Do thang máy bị hư nên bạn Vy đi bộ bắt đầu từ tầng 1 về căn hộ của mình. Tổng số bậc thang Vy đã đi là 135. Hỏi căn hộ của Vy ở tầng thứ bao nhiêu của tòa nhà?

Bài 4: (1 điểm) Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt nước biển một góc\({21^o}\). Nếu tàu chuyển động theo phương lặn xuống được 300m thì nó ở độ sâu bao nhiêu? Khi đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu mét ? (kết quả làm tròn đến mét)

Bài 5: (3,0 điểm) Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính AB . Vẽ các tiếp tuyến \(Ax\) và \(By\) của đường tròn \(\left( {O;R} \right)\).

a)Chứng minh: \(Ax//By\).

b)Trên \(\left( {O;R} \right)\)lấy điểm M . Tiếp tuyến tại M của đường tròn \(\left( {O;R} \right)\)lần lượt cắt \(Ax\) và \(By\) tại D và E . Chứng minh: \(DE = DA + BE\).

c)Chứng minh: \(\angle DOE = {90^o}\) và \(DA.BE = {R^2}\).

LG bài 1

Lời giải chi tiết:

a)Tính chu vi tam giác ABC biết độ dài 3 cạnh là \(AB = 5\sqrt 2 \left( {cm} \right),AC = \sqrt {32} \left( {cm} \right)\) , \(BC = \sqrt {98} \left( {cm} \right)\) . (Không yêu cầu vẽ hình)

Chu vi của tam giác ABC là:

\(\begin{array}{l}AB + AC + BC = 5\sqrt 2  + \sqrt {32}  + \sqrt {98}  = 5\sqrt 2  + \sqrt {{4^2}.2}  + \sqrt {{7^2}.2} \\ = 5\sqrt 2  + 4\sqrt 2  + 7\sqrt 2  = 16\sqrt 2 .\end{array}\)

Vậy tam giác có chu vi là \(16\sqrt 2 \).\(\)

b)Thu gọn: \(B = \sqrt {{{\left( {\sqrt 7  - 1} \right)}^2}}  - \dfrac{6}{{\sqrt 7  - 1}}\) .

\(\begin{array}{l}B = \sqrt {{{\left( {\sqrt 7  - 1} \right)}^2}}  - \dfrac{6}{{\sqrt 7  - 1}} \\\;\;\;= \left| {\sqrt 7  - 1} \right| - \dfrac{{6\left( {\sqrt 7  + 1} \right)}}{{\left( {\sqrt 7  - 1} \right)\left( {\sqrt 7  + 1} \right)}}\\\;\;\; = \sqrt 7  - 1 - \dfrac{{6\left( {\sqrt 7  + 1} \right)}}{{{{\left( {\sqrt 7 } \right)}^2} - 1}} \\\;\;\;= \sqrt 7  - 1 - \left( {\sqrt 7  + 1} \right)\\\;\;\; = \sqrt 7  - 1 - \sqrt 7  - 1 =  - 2.\end{array}\)

Vậy \(B =  - 2\).

LG bài 2

Lời giải chi tiết:

Cho đường thẳng \(\left( {{d_1}} \right):y =  - 3x + 1\) và đường thẳng \(\left( {{d_2}} \right):y = x - 3\) .

a)Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng mặt phẳng tọa độ \(Oxy\) .

Ta có bảng giá trị:

Vậy đường thẳng \(\left( {{d_1}} \right)\) đi qua điểm \(\left( {0;\;1} \right),\;\;\left( {1; - 2} \right)\) và đường thẳng \(\left( {{d_2}} \right)\) đi qua điểm \(\left( {0; - 3} \right),\;\;\left( {1; - 2} \right).\)

Từ đó ta có đồ thị của hai hàm số:

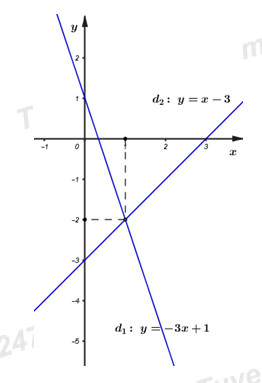
b)Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng phép tính.

Hoành độ giao điểm của hai đường thẳng là nghiệm của phương trình :

\( - 3x + 1 = x - 3 \Leftrightarrow 4x = 4 \Leftrightarrow x = 1\).

Với \(x = 1 \Rightarrow y = x - 3 = 1 - 3 =  - 2\)

Vậy tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\)là: \(A\left( {1; - 2} \right)\).\(\)

c)Tìm \(m\) để đường thẳng \(\left( D \right):y = \left( {2m + 3} \right)x - 5\) song song với đường thẳng \(\left( {{d_1}} \right)\) .

Hai đường thẳng song song khi chúng có cùng hệ số góc và chúng không trùng nhau. Suy ra để

đường thẳng \(\left( D \right):y = \left( {2m + 3} \right)x - 5\) song song với đường thẳng \(\left( {{d_1}} \right)\) thì:

\(\left\{ \begin{array}{l}2m + 3 =  - 3\\ - 5 \ne 1\end{array} \right. \)

\(\Leftrightarrow \left\{ \begin{array}{l}2m =  - 6\\ - 5 \ne 1\end{array} \right. \Leftrightarrow m =  - 3\).

Vậy \(m =  - 3\) là giá trị cần tìm.

LG bài 3

Lời giải chi tiết:

Bài 3:Trong một tòa nhà ngoài thang máy người ta còn xây thêm một cầu thang đi bộ. Từ tầng 1 đến tầng 2 có 30 bậc thang. Các tầng còn lại cứ hai tầng liên tiếp cách nhau 21 bậc thang. Do thang máy bị hư nên bạn Vy đi bộ bắt đầu từ tầng 1 về căn hộ của mình. Tổng số bậc thang Vy đã đi là 135. Hỏi căn hộ của Vy ở tầng thứ bao nhiêu của tòa nhà?

Giả sử nhà bạn Vy ở tầng thứ \(n\) của tòa nhà\(\left( {n > 1,\;n \in {N^*}} \right).\)

Suy ra sốtầng  mà bạn Vy phải đi là \(n - 1\)tầng.

\( \Rightarrow \)số tầng mà bạn Vy phải đi có  21 bậc thang là: \(n - 2\) (do cầu thang tầng 1 có 30 bậc thang)

Suy ra số bậc thang mà bạn Vy phải đi bộ là: \(30 + 21.\left( {n - 2} \right)\) bậc.

Theo đề bài ta có phương trình:

\(30 + 21\left( {n - 2} \right) = 135 \Leftrightarrow n - 2 = 5 \Leftrightarrow n = 7\;\;\left( {tm} \right)\).

Vậy nhà bạn Vy ở tầng 7 của tòa nhà.\(\)

LG bài 4

Lời giải chi tiết:

Bài 4:Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt nước biển một góc \({21^o}\) . Nếu tàu chuyển động theo phương lặn xuống được 300m thì nó ở độ sâu bao nhiêu? Khi đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu mét ? (kết quả làm tròn đến mét)

Coi mặt biển là một mặt phẳng, theo đề bài ta có hình vẽ minh họa:

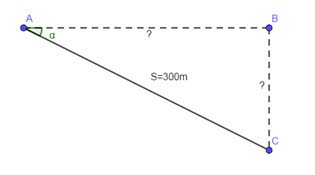
Trong hình vẽ ta có:

+)  Đoạn AC là quãng đường tàu di chuyển trong quá trình lặn,

+) Đoạn BC là độ sâu mà tàu lặn được.

+) Đoạn AB là khoảng cách theo phương ngang tính từ vị trí xuất phát tới vị trí của tàu sau khi lặn.

+) \(\alpha \) là góc tạo bởi quãng đường tàu chuyển động và mặt biển.

Xét tam giác vuông ABC vuông tại B có:

+) \(\sin \alpha  = \dfrac{{BC}}{{AC}}\) \( \Rightarrow BC = AC.\sin \alpha  = 300.\sin {21^o} \approx 107\left( m \right)\)

+) \(\cos \alpha  = \dfrac{{AB}}{{AC}}\) \( \Rightarrow AB = AC.\cos \alpha  = 300.cos{21^o} = 280\left( m \right)\)

Vậy tàu lặn xuống độ sâu 107 (m) và khoảng cách theo phương ngang từ vị trí ban đầu tới vị trí sau khi lặn là 280 (m).

LG bài 6

Lời giải chi tiết:

Bài 5:Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính AB . Vẽ các tiếp tuyến \(Ax\) và \(By\) của đường tròn \(\left( {O;R} \right)\) .

a)Chứng minh: \(Ax//By\) .

Xét đường tròn \(\left( {O;R} \right)\)có \(Ax\) là tiếp tuyến với A là tiếp điểm.

\( \Rightarrow Ax \bot OA\)(tính chất tiếp tuyến)\( \Rightarrow Ax \bot AB\)(do OA nằm trên AB )\(\)

Chứng minh tương tự có \(By \bot AB\)

Suy ra \(Ax//By\) (do cùng vuông góc với AB )(đpcm).\(\)

b)Trên \(\left( {O;R} \right)\) lấy điểm M . Tiếp tuyến tại M của đường tròn \(\left( {O;R} \right)\) lần lượt cắt \(Ax\) và \(By\) tại D và E . Chứng minh: \(DE = DA + BE\) .

Xét \(\left( {O;R} \right)\)có DM , AD là tiếp tuyến với A , M là tiếp điểm

\( \Rightarrow AD = DM\)(tính chất tiếp tuyến)                                          (1)

Tương tự ta có: \(ME = BE\)                                                 (2)

Vì M nằm trên đoạn DE nên ta có: \(DE = DM + ME\)                    (3)

Từ (1) , (2) , (3) suy ra\(DE = DA + BE\)(đpcm).

c)Chứng minh: \(\angle DOE = {90^o}\) và \(DA.BE = {R^2}\) .

+)Chứng minh \(\angle DOE = {90^o}\)

Có: \(DM = DA\)(cmt), suy ra D cách đều A và M , suy ra D nằm trên đường trung trực của AM

Mà có: \(OA = OM\) (cùng là bán kính) suy ra O cách đều A và M , suy ra O nằm trên trung trực của AM

Suy ra OD là trung trực của AM , suy ra \(OD \bot AM.\)

Chứng minh tương tự có \(OE \bot MB.\)

Xét tứ giác MCOF có:

+) \(\angle MCO = {90^o}\) (do \(OD \bot AM\))

+)  \(\angle MFO = {90^o}\)(do \(OE \bot MB\))

+)  \(\angle CMF = {90^o}\)(do là góc nội tiếp chắn nửa đường tròn)

Suy ra MCOF là hình chữ nhật (dhnb), suy ra \(\angle DOE = {90^o}\). (đpcm)

+) Chứng minh \(DA.BE = {R^2}\).

Xét tam giác DOE vuông tại O có: OM là đường cao (do DE là tiếp tuyến nên OM vuông góc với DE )

\( \Rightarrow ME.MD = O{M^2}\)

Mà có: \(\left\{ \begin{array}{l}DA = MD\\BE = ME\end{array} \right.\) (cmt)

Suy ra \(DA.BE = {R^2}\) (đpcm).