Đề số 8 - Đề kiểm tra học kì 1 - Toán 9 — Không quảng cáo

Đề bài

Bài 1: (1 điểm) Thực hiện phép tính:

1) $A = \sqrt {12}  - 2\sqrt {48}  + \dfrac{7}{5}\sqrt {75}$

2) $B = \sqrt {14 - 6\sqrt 5 }  + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}}$

Bài 2: (2,5 điểm)

1)Cho biểu thức $A = \dfrac{{\sqrt x  + 4}}{{\sqrt x  + 2}}\left( {x \ge 0} \right)$. Tính giá trị biểu thức $A$ khi $x = 36$.

2)Rút gọn biểu thức $B = \left( {\dfrac{{\sqrt x }}{{\sqrt x  + 4}} + \dfrac{4}{{\sqrt x  - 4}}} \right):\dfrac{{x + 16}}{{\sqrt x  + 2}}$ (với $x \ge 0,x \ne 16$).

3)Với các biểu thức $A,B$nói trên, hãy tìm các giá trị nguyên của $x$ để giá trị của biểu thức $P = B\left( {A - 1} \right)$là số nguyên.

Bài 3: (1,5 điểm) Cho hàm số $y = 2x + 4$ có đồ thị là $\left( {{d_1}} \right)$và hàm số $y =  - x + 1$ có đồ thị là $\left( {{d_2}} \right)$

1)Vẽ $\left( {{d_1}} \right)$và $\left( {{d_2}} \right)$ trên cùng một mặt phẳng tọa độ .

2)Gọi A là giao điểm của $\left( {{d_1}} \right)$và $\left( {{d_2}} \right)$. Tìm tọa độ của điểm A .

3)Xác định các hệ số $a,b$ của đường thẳng ${d_3}:y = ax + b$. Biết rằng $\left( {{d_3}} \right)$song song với $\left( {{d_1}} \right)$ và $\left( {{d_3}} \right)$cắt $\left( {{d_2}} \right)$ tại một điểm có hoành độ bằng 2.

Bài 4: (4,5 điểm)

1)Cho tam giác ABC vuông tại A có AH là đường cao. Biết $BH = 9$cm, $HC = 16$cm. Tính độ dài AH, AC , số đo $\angle ABC$ (số đo làm tròn đến độ).

2)Cho nửa đường tròn tâm O đường kính AB . Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, kẻ hai tiếp tuyến Ax, By với nửa đường tròn, M là một điểm nằm trên nửa đường tròn ( M khác A và B ), từ M kẻ tiếp tuyến với nửa đường tròn cắt Ax, By lần lượt tại C và D.

a)Chứng minh rằng: $CD = AC + BD$

b) AM cắt OC tại E, BM cắt OD tại F. Chứng minh $EF = OM$.

c)Chứng minh rằng tích $AC.BD$ không phụ thuộc vào vị trí của điểm M.

d)Kẻ MH vuông góc với AB tại H, MH cắt BC tại I. Chứng minh rằng I là trung điểm của MH.

Bài 5: (0,5 điểm)

Cho $a,b,c$là các số dương thỏa mãn điều kiện $a + b + c + ab + bc + ca = 6$. Chứng minh rằng:  $\dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge {a^2} + {b^2} + {c^2} \ge 3$

LG bài 1

Lời giải chi tiết:

Bài 1: Thực hiện phép tính:

$\begin{array}{l}1)\;\;A = \sqrt {12}  - 2\sqrt {48}  + \dfrac{7}{5}\sqrt {75} \\\;\;\; = \sqrt {{2^2}.3}  - 2\sqrt {{4^2}.3}  + \dfrac{7}{5}\sqrt {{5^2}.3} \\\;\;\; = 2\sqrt 3  - 2.4\sqrt 3  + \dfrac{7}{5}.5\sqrt 3  = \sqrt 3 .\end{array}$

Vậy $A = \sqrt 3$.

$\begin{array}{l}2)\;\;B = \sqrt {14 - 6\sqrt 5 }  + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \\\;\;\;\;\;\;\; = \sqrt {{3^2} + 2.3.\sqrt 5  + {{\left( {\sqrt 5 } \right)}^2}}  + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \\\;\;\;\;\;\;\; = \sqrt {{{\left( {3 + \sqrt 5 } \right)}^2}}  + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \\\;\;\;\;\;\;\; = \left| {3 + \sqrt 5 } \right| + \left| {2 - \sqrt 5 } \right|\\\;\;\;\;\;\;\; = 3 + \sqrt 5  + \sqrt 5  - 2\; = 2\sqrt {5 + 1} .\;\;\;\left( {do\;\;\;\sqrt 5  - 2 > 0} \right)\end{array}$

Vậy $B = 2\sqrt 5  + 1$

LG bài 2

Lời giải chi tiết:

1)Cho biểu thức $A = \dfrac{{\sqrt x  + 4}}{{\sqrt x  + 2}}\left( {x \ge 0} \right)$. Tính giá trị biểu thức $A$ khi $x = 36$.

Thay $x = 36$ vào biểu thức ta có: $A = \dfrac{{\sqrt {36}  + 4}}{{\sqrt {36}  + 2}} = \dfrac{{6 + 4}}{{6 + 2}} = \dfrac{5}{4}$.

Vậy khi $x = 36$thì $A = \dfrac{5}{4}$.

2)Rút gọn biểu thức $B = \left( {\dfrac{{\sqrt x }}{{\sqrt x  + 4}} + \dfrac{4}{{\sqrt x  - 4}}} \right):\dfrac{{x + 16}}{{\sqrt x  + 2}}$ (với $x \ge 0,x \ne 16$).

ĐKXĐ: $x \ge 0,x \ne 16$

$\begin{array}{l}B = \left( {\dfrac{{\sqrt x }}{{\sqrt x  + 4}} + \dfrac{4}{{\sqrt x  - 4}}} \right):\dfrac{{x + 16}}{{\sqrt x  + 2}}\\\;\;\; = \left( {\dfrac{{\sqrt x \left( {\sqrt x  - 4} \right)}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}} + \dfrac{{4\left( {\sqrt x  + 4} \right)}}{{\left( {\sqrt x  + 4} \right)\left( {\sqrt x  - 4} \right)}}} \right):\dfrac{{x + 16}}{{\sqrt x  + 2}}\\\;\;\; = \dfrac{{x - 4\sqrt x  + 4\sqrt x  + 16}}{{{{\left( {\sqrt x } \right)}^2} - {4^2}}}.\dfrac{{\sqrt x  + 2}}{{x + 16}} = \dfrac{{\sqrt x  + 2}}{{x - 16}}\end{array}$

Vậy $B = \dfrac{{\sqrt x  + 2}}{{x - 16}}$.

3)Với các biểu thức $A,B$nói trên, hãy tìm các giá trị nguyên của $x$ để giá trị của biểu thức $P = B\left( {A - 1} \right)$là số nguyên.

ĐKXĐ: $x \ge 0,x \ne 16$. Với điều kiện trên ta có:

$P = B\left( {A - 1} \right) = \dfrac{{\sqrt x  + 2}}{{x - 16}}.\left( {\dfrac{{\sqrt x  + 4}}{{\sqrt x  + 2}} - 1} \right) = \dfrac{{\sqrt x  + 2}}{{x - 16}}.\dfrac{{\sqrt x  + 4 - \left( {\sqrt x  + 2} \right)}}{{\sqrt x  + 2}} = \dfrac{2}{{x - 16}}.$

Để biểu thức $P$ nguyên thì $x - 16$ phải là ước của 2

$\Rightarrow \left\{ \begin{array}{l}x \ge 0,x \ne 16\\\left[ \begin{array}{l}x - 16 = 2\\x - 16 =  - 2\\x - 16 = 1\\x - 16 =  - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0,x \ne 16\\\left[ \begin{array}{l}x = 18\\x = 14\\x = 15\\x = 17\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 18\\x = 14\\x = 15\\x = 17\end{array} \right.$

Vậy với $x = 18,x = 17,x = 15,x = 14$ thì giá trị của biểu thức $P = B\left( {A - 1} \right)$là số nguyên.

LG bài 3

Lời giải chi tiết:

Cho hàm số $y = 2x + 4$ có đồ thị là $\left( {{d_1}} \right)$và hàm số $y =  - x + 1$ có đồ thị là $\left( {{d_2}} \right)$

1)Vẽ $\left( {{d_1}} \right)$và $\left( {{d_2}} \right)$ trên cùng một mặt phẳng tọa độ .

+) Nhận thấy hai điểm $A\left( { - 1;2} \right),B\left( { - 2;0} \right)$ thuộc đồ thị hàm số $y = 2x + 4$.

+) Nhận thấy hai điểm $A\left( { - 1;2} \right),C\left( {0;1} \right)$thuộc đồ thị hàm số $y =  - x + 1$.

Từ đó ta có đồ thị của hai hàm số:

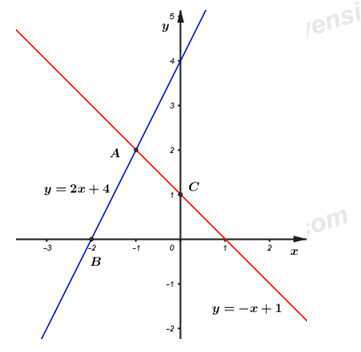
2)Gọi A là giao điểm của $\left( {{d_1}} \right)$và $\left( {{d_2}} \right)$. Tìm tọa độ của điểm A.

Hoành độ giao điểm của $\left( {{d_1}} \right)$và $\left( {{d_2}} \right)$là nghiệm của phương trình:

$2x + 4 =  - x + 1 \Leftrightarrow 3x =  - 3 \Leftrightarrow x =  - 1$

Với $x =  - 1 \Rightarrow y = 2x + 4 = 2.\left( { - 1} \right) + 4 = 2$

Vậy giao điểm của $\left( {{d_1}} \right)$và $\left( {{d_2}} \right)$ là $A\left( { - 1;2} \right)$

3)Xác định các hệ số $a,b$ của đường thẳng ${d_3}:y = ax + b$. Biết rằng $\left( {{d_3}} \right)$song song với $\left( {{d_1}} \right)$ và $\left( {{d_3}} \right)$cắt $\left( {{d_2}} \right)$ tại một điểm có hoành độ bằng 2.

Vì $\left( {{d_3}} \right)$song song với $\left( {{d_1}} \right)$nên hai đường thẳng này có hệ số góc bằng nhau$\Rightarrow \left\{ \begin{array}{l}a = 2\\b \ne 4\end{array} \right..$

Điểm thuộc $\left( {{d_2}} \right)$ có hoành độ bằng 2 là $\left( {2; - 1} \right)$. Vì $\left( {{d_3}} \right)$cắt $\left( {{d_2}} \right)$ tại một điểm có hoành độ bằng 2 nên điểm$\left( {2; - 1} \right)$ thuộc đồ thị hàm số ${d_3}:y = ax + b$

$\begin{array}{l} \Rightarrow  - 1 = a.2 + b\\ \Rightarrow b =  - 1 - 2a =  - 1 - 2.2 =  - 5\;\;\left( {tm} \right)\end{array}$

Vậyb$a = 2,b =  - 5$.

LG bài 4

Lời giải chi tiết:

Bài 4: (4,5 điểm)

1)Cho tam giác ABC vuông tại A có AH là đường cao. Biết $BH = 9$cm, $HC = 16$cm. Tính độ dài AH, AC, số đo $\angle ABC$ (số đo làm tròn đến độ).

Xét tam giác ABC vuông tại A có AH là đường cao.

Áp dụng hệ thức lượng trong tam giác vuông ta có:

$\begin{array}{l} + )A{H^2} = BH.HC \Rightarrow AH = \sqrt {9.16}  = 12\\ + )A{C^2} = CH.BC = CH.\left( {CH + BH} \right) \Rightarrow AC = \sqrt {16.\left( {9 + 16} \right)}  = 20\end{array}$

Xét tam giác ABC vuông tại A có:

$\sin \left( {\angle ABC} \right) = \dfrac{{AC}}{{BC}} = \dfrac{{AC}}{{CH + BH}} = \dfrac{{20}}{{16 + 9}} = \dfrac{4}{5} \Rightarrow \angle ABC = \arcsin \dfrac{4}{5} \approx {53^o}$.

2)Cho nửa đường tròn tâm O đường kính AB . Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, kẻ hai tiếp tuyến Ax, By với nửa đường tròn, M là một điểm nằm trên nửa đường tròn ( M khác A và B ), từ M kẻ tiếp tuyến với nửa đường tròn cắt Ax, By lần lượt tại C và D .

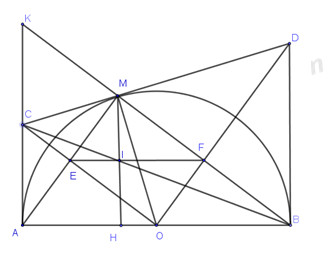
a)Chứng minh rằng: $CD = AC + BD$

Xét nửa đường tròn tâm O đường kính AB có AC và MC là hai tiếp tuyến giao nhau tại M với M,A là tiếp điểm$\Rightarrow AC = MC$(tính chất tiếp tuyến)

Chứng minh tương tự ta có$MD = BD$.

Vì M nằm trên đoạn CD nên$CD = MD + MC$. Mà có$AC = CM,BD = MD$ (cmt)

Suy ra $CD = AC + BD$ (đpcm).

b) AM cắt OC tại E, BM cắt OD tại F. Chứng minh $EF = OM$.

Có:$MD = BD$(cmt) suy ra D nằm trên đường trung trực của MB (do cách đều hai điểm M, B )

Có: $OM = OB$(do cùng là bán kính) suy ra O nằm trên trung trực của MB (do cách đều M, B )

Suy ra OD là trung trực của MB , suy ra $OD \bot MB.$

Chứng minh tương tự có $OC \bot AM.$

Xét tứ giác MEOF có:

+) $\angle AMB = {90^o}$ (góc nội tiếp chắn nửa đường tròn)

+) $\angle MEO = {90^o}$ (do $OC \bot AM$)

+) $\angle MFO = {90^o}$(do $OD \bot MB$)

Suy ra tứ giác MEOF là hình chữ nhật (do có 3 góc vuông), suy ra $EF = MO$(hình chữ nhật có hai đường chéo bằng nhau). (đpcm)

c)Chứng minh rằng tích $AC.BD$ không phụ thuộc vào vị trí của điểm M .

Vì MEOF là hình chữ nhật nên$\angle FOE = {90^o}$, suy ra tam giác COD vuông tại O .

Xét tam giác COD vuông tại O có OM là đường cao ($OM \bot CD$do CD là tiếp tuyến với đường tròn)

$\Rightarrow CM.MD = O{M^2}$(hệ thức lượng trong tam giác vuông)

Mà có: $CM = AC,\;\;MD = BD$(cmt)

$\Rightarrow AC.BD = O{M^2} = {R^2}$.

$\Rightarrow AC.BD$luôn không đổi với mọi vị trí của điểm M .

d)Kẻ MH vuông góc với AB tại H, MH cắt BC tại I. Chứng minh rằng I là trung điểm của MH .

Kéo dài MB cắt AC tại K.

Có: $\angle CKM = \angle DBM$(do AC song song với BD )                                            (1)

Có: $\angle KMC = \angle DMB$(hai góc đối đỉnh)                                                           (2)

Mà có tam giác MBD cân tại D (do $MD = BD$) nên $\angle DMB = \angle DBM$       (3)

Từ (1), (2), (3) ta có: $\angle CKM = \angle KMC$, suy ra tam giác KMC cân tại C , suy ra $KC = CM$.

Mà có: $CA = CM$ (cmt)

$\Rightarrow CK = AC = \dfrac{1}{2}AK$.

Xét tam giác KBC có: MI song song với KC (do cùng vuông góc với AB )

$\Rightarrow \dfrac{{MI}}{{KC}} = \dfrac{{BM}}{{BK}}$ (định lí Ta-lét)                                (4)

Xét tam giác ABK có MH song song với AK (do cùng vuông góc với AB )

$\Rightarrow \dfrac{{MH}}{{AK}} = \dfrac{{BM}}{{BK}}$ (định lí Ta-lét)                               (5)

Từ (4) và (5) suy ra $\dfrac{{MI}}{{KC}} = \dfrac{{MH}}{{AK}}$. Mà có $KC = \dfrac{1}{2}AK$ (cmt)

$\Rightarrow MI = \dfrac{1}{2}MH \Rightarrow IH = MH - MI = MH - \dfrac{1}{2}MH = \dfrac{1}{2}MH \Rightarrow MH = MI$

Vậy I là trung điểm của IH (đpcm).

LG bài 5

Lời giải chi tiết:

Bài 5:

Cho $a,b,c$là các số dương thỏa mãn điều kiện $a + b + c + ab + bc + ca = 6$. Chứng minh rằng:  $\dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge {a^2} + {b^2} + {c^2} \ge 3$.

+) Chứng minh bất đẳng thức phụ: Với $a,b,c$là các số dương ta có:

$\left\{ \begin{array}{l}\dfrac{{{a^2}}}{2} + \dfrac{{{b^2}}}{2} \ge 2\sqrt {\dfrac{{{a^2}}}{2}.\dfrac{{{b^2}}}{2}}  = ab\\\dfrac{{{b^2}}}{2} + \dfrac{{{c^2}}}{2} \ge 2\sqrt {\dfrac{{{b^2}}}{2}.\dfrac{{{c^2}}}{2}}  = bc\\\dfrac{{{c^2}}}{2} + \dfrac{{{a^2}}}{2} \ge 2\sqrt {\dfrac{{{c^2}}}{2}.\dfrac{{{a^2}}}{2}}  = ac\end{array} \right.$ $\Rightarrow 2\left( {\dfrac{{{a^2}}}{2} + \dfrac{{{b^2}}}{2} + \dfrac{{{c^2}}}{2}} \right) \ge ab + bc + ca \Rightarrow {a^2} + {b^2} + {c^2} \ge ab + bc + ca$

Từ bất đẳng thức trên ta dễ chứng minh được bất đẳng thức thứ hai.

Ta có:

$\begin{array}{l}\;\;\;\;{a^2} + {b^2} + {c^2} \ge ab + bc + ca\\ \Leftrightarrow {a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca \ge 3\left( {ab + bc + ca} \right)\\ \Leftrightarrow {\left( {a + b + c} \right)^2} \ge 3\left( {ab + bc + ca} \right)\end{array}$

+) Xét bất đẳng thức $\dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge {a^2} + {b^2} + {c^2}$

Áp dụng bất đẳng thức Co-si ta có:

$\begin{array}{l} + )\dfrac{{{a^3}}}{b} + ab \ge 2\sqrt {\dfrac{{{a^3}}}{b}.ab}  = 2{a^2}\\ + )\dfrac{{{b^3}}}{c} + bc \ge 2\sqrt {\dfrac{{{b^3}}}{c}.bc}  = 2{b^2}\\ + )\dfrac{{{c^3}}}{a} + ac \ge 2\sqrt {\dfrac{{{c^3}}}{a}.ac}  = 2{c^2}\\ \Rightarrow \dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge 2\left( {{a^2} + {b^2} + {c^2}} \right) - \left( {ab + bc + ca} \right) = {a^2} + {b^2} + {c^2} + \left[ {{a^2} + {b^2} + {c^2} - \left( {ab + bc + ca} \right)} \right]\end{array}$

Mà có: ${a^2} + {b^2} + {c^2} \ge ab + bc + ca \Rightarrow {a^2} + {b^2} + {c^2} - \left( {ab + bc + ca} \right) \ge 0$

$\begin{array}{l} \Rightarrow {a^2} + {b^2} + {c^2} + \left( {{a^2} + {b^2} + {c^2} - \left( {ab + bc + ca} \right)} \right) \ge {a^2} + {b^2} + {c^2}\\ \Rightarrow \dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge {a^2} + {b^2} + {c^2}\end{array}$

Xét bất đẳng thức: ${a^2} + {b^2} + {c^2} \ge 3$

Theo đề bài có: $a + b + c + ab + bc + ca = 6$

Mà có: $ab + bc + ca \le \dfrac{{{{\left( {a + b + c} \right)}^2}}}{3}$ (cmt)

$\begin{array}{l} \Rightarrow \left( {a + b + c} \right) + \dfrac{{{{\left( {a + b + c} \right)}^2}}}{3} \ge 6 \Leftrightarrow {\left( {a + b + c} \right)^2} + 3\left( {a + b + c} \right) - 18 \ge 0\\ \Leftrightarrow \left( {a + b + c - 3} \right)\left( {a + b + c + 6} \right) \ge 0 \Leftrightarrow a + b + c \ge 3\end{array}$

Do $a,b,c > 0 \Rightarrow a + b + c + 6 > 0$

Áp dụng bất đẳng thức Bunhiacopski cho bộ ba số $\left( {1;1;1} \right)$ và $\left( {a;b;c} \right)$ có:

$\left( {{1^2} + {1^2} + {1^2}} \right)\left( {{a^2} + {b^2} + {c^2}} \right) \ge {\left( {a.1 + b.1 + c.1} \right)^2} \Leftrightarrow {a^2} + {b^2} + {c^2} \ge \dfrac{{{{\left( {a + b + c} \right)}^2}}}{3} \ge \dfrac{{{3^2}}}{3} = 3$.

Vậy ta chứng minh được $\dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge {a^2} + {b^2} + {c^2} \ge 3$.