Đề thi giữa kì 1 Toán 6 - Đề số 18
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Đề bài
Theo Âm Lịch, năm 2024 là năm Giáp Thìn, tức năm con Rồng – xếp thứ năm trong 12 con giáp. Năm Giáp Thìn sẽ bắt đầu từ ngày 10/02/2024 và kết thúc năm vào ngày 28/01/2025 theo lịch dương. Gọi A là tập hợp các chữ số xuất hiện ở hình bên. Khi đó

-
A.
\(A = \left\{ {4;2;0;2} \right\}\).
-
B.
\(A = \left\{ {2;0;2;4} \right\}\).
-
C.
\(A = \left\{ {0;2;4} \right\}\).
-
D.
\(A = \left\{ {0;2} \right\}\).
Cho tập hợp \(A = \left\{ {1;\,\,2;\,\,a;\,\,b} \right\}\). Khẳng định nào dưới đây sai ?
-
A.
\(1 \in A\).
-
B.
\(a \in A\).
-
C.
\(5 \notin A\).
-
D.
\(b \notin A\).
Cho số tự nhiên x, biết \(x + 20 = 55\). Khi đó
-
A.
\(x = 20\).
-
B.
\(x = 25\).
-
C.
\(x = 30\).
-
D.
\(x = 35\).
Phép tính \({3^{40}}{.3^{200}}:{3^{50}}\) có kết quả là:
-
A.
\({3^{54}}\).
-
B.
\({3^{100}}\).
-
C.
\({3^{50}}\).
-
D.
\({3^{190}}\).
Kết quả của phép tính \(37.64 + 37.36\) là
-
A.
3700.
-
B.
3600.
-
C.
370.
-
D.
6400.
Trong các số tự nhiên sau số nào là số nguyên tố?
-
A.
1.
-
B.
5.
-
C.
9.
-
D.
12.
Khẳng định nào sau đây là đúng ?
-
A.
Số 2 là số nguyên tố chẵn duy nhất.
-
B.
Số 0 là số nguyên tố.
-
C.
Các số nguyên tố nhỏ hơn 10 là 3; 5; 7; 9 .
-
D.
Các số nguyên tố đều là số lẻ.
Tổng chia hết cho 3 là:
-
A.
145 + 207.
-
B.
875 + 27.
-
C.
379 + 978.
-
D.
207 + 708.
-
A.
HÌNH 1.
-
B.
HÌNH 2.
-
C.
HÌNH 3.
-
D.
HÌNH 4.
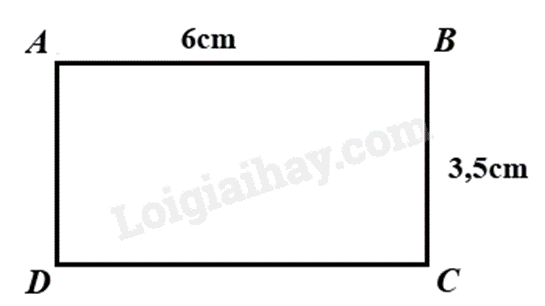
-
A.
Cạnh AD và cạnh BA song song với nhau.
-
B.
CD = 6cm.
-
C.
BD = 3,5cm.
-
D.
Cạnh AC và cạnh BD song song với nhau.
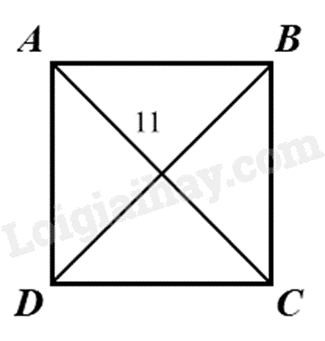
-
A.
BD = 10cm.
-
B.
BD = 9cm.
-
C.
BD = 11cm.
-
D.
BD = 12cm.
Hình bình hành không có tính chất nào sau đây?
-
A.
Hai cạnh đối song song với nhau.
-
B.
Hai cạnh đối bằng nhau.
-
C.
Bốn cạnh bằng nhau.
-
D.
Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Lời giải và đáp án
Theo Âm Lịch, năm 2024 là năm Giáp Thìn, tức năm con Rồng – xếp thứ năm trong 12 con giáp. Năm Giáp Thìn sẽ bắt đầu từ ngày 10/02/2024 và kết thúc năm vào ngày 28/01/2025 theo lịch dương. Gọi A là tập hợp các chữ số xuất hiện ở hình bên. Khi đó

-
A.
\(A = \left\{ {4;2;0;2} \right\}\).
-
B.
\(A = \left\{ {2;0;2;4} \right\}\).
-
C.
\(A = \left\{ {0;2;4} \right\}\).
-
D.
\(A = \left\{ {0;2} \right\}\).
Đáp án : C
Dựa vào kiến thức về tập hợp.
Trong hình có các số 2; 0; 4 xuất hiện nên tập A là: \(A = \left\{ {0;2;4} \right\}\).
Đáp án C.
Cho tập hợp \(A = \left\{ {1;\,\,2;\,\,a;\,\,b} \right\}\). Khẳng định nào dưới đây sai ?
-
A.
\(1 \in A\).
-
B.
\(a \in A\).
-
C.
\(5 \notin A\).
-
D.
\(b \notin A\).
Đáp án : D
Xác định phần tử thuộc và không thuộc tập hợp.
Tập hợp A có các phần tử 1; 2; a; b nên đáp án A, B đúng, D sai.
5 không thuộc tập A nên C. \(5 \notin A\) đúng.
Đáp án D.
Cho số tự nhiên x, biết \(x + 20 = 55\). Khi đó
-
A.
\(x = 20\).
-
B.
\(x = 25\).
-
C.
\(x = 30\).
-
D.
\(x = 35\).
Đáp án : D
Sử dụng quy tắc chuyển vế để tìm x.
Ta có:
\(\begin{array}{l}x + 20 = 55\\x = 55 - 20\\x = 35\end{array}\)
Đáp án D.
Phép tính \({3^{40}}{.3^{200}}:{3^{50}}\) có kết quả là:
-
A.
\({3^{54}}\).
-
B.
\({3^{100}}\).
-
C.
\({3^{50}}\).
-
D.
\({3^{190}}\).
Đáp án : D
Nhân hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\).
Chia hai lũy thừa cùng cơ số: \({a^m}:{a^n} = {a^{m - n}}\left( {a \ne 0;m \ge n \ge 0} \right)\).
Ta có:
\({3^{40}}{.3^{200}}:{3^{50}} = {3^{40 + 200 - 50}} = {3^{190}}\).
Đáp án D.
Kết quả của phép tính \(37.64 + 37.36\) là
-
A.
3700.
-
B.
3600.
-
C.
370.
-
D.
6400.
Đáp án : A
Sử dụng tính chất phân phối của phép nhân với phép cộng.
Ta có:
\(37.64 + 37.36 = 37\left( {64 + 36} \right) = 37.100 = 3700\).
Đáp án A.
Trong các số tự nhiên sau số nào là số nguyên tố?
-
A.
1.
-
B.
5.
-
C.
9.
-
D.
12.
Đáp án : B
Số nguyên tố là các số chỉ có 2 ước là 1 và chính nó.
Trong các số trên chỉ có 5 là số nguyên tố.
Đáp án B.
Khẳng định nào sau đây là đúng ?
-
A.
Số 2 là số nguyên tố chẵn duy nhất.
-
B.
Số 0 là số nguyên tố.
-
C.
Các số nguyên tố nhỏ hơn 10 là 3; 5; 7; 9 .
-
D.
Các số nguyên tố đều là số lẻ.
Đáp án : A
Dựa vào kiến thức về số nguyên tố.
Chỉ có số 2 là số nguyên tố chẵn duy nhất nên A là khẳng định đúng.
Số 0 không phải số nguyên tố nên B sai.
Số 9 có 3 ước là 1; 3; 9, không phải số nguyên tố nên C sai.
Số 2 là số nguyên tố chẵn nên D sai.
Đáp án A.
Tổng chia hết cho 3 là:
-
A.
145 + 207.
-
B.
875 + 27.
-
C.
379 + 978.
-
D.
207 + 708.
Đáp án : D
Sử dụng dấu hiệu chia hết cho 3 tính chất chia hết của một tổng.
A. \(145\not{ \vdots }3\) và \(207 \vdots 3\) nên \(\left( {145 + 207} \right)\not{ \vdots }3\).
B. \(875\not{ \vdots }3\) và \(27 \vdots 3\) nên \(\left( {875 + 27} \right)\not{ \vdots }3\).
C. \(379\not{ \vdots }3\) và \(978 \vdots 3\) nên \(\left( {379 + 978} \right)\not{ \vdots }3\).
D. \(207 \vdots 3\) và \(708 \vdots 3\) nên \(\left( {207 + 708} \right) \vdots 3\).
Đáp án D.
-
A.
HÌNH 1.
-
B.
HÌNH 2.
-
C.
HÌNH 3.
-
D.
HÌNH 4.
Đáp án : A
Tam giác đều có 3 cạnh bằng nhau.
Ta thấy HÌNH 1 là tam giác có 3 cạnh bằng nhau nên là tam giác đều.
Đáp án A.
-
A.
Cạnh AD và cạnh BA song song với nhau.
-
B.
CD = 6cm.
-
C.
BD = 3,5cm.
-
D.
Cạnh AC và cạnh BD song song với nhau.
Đáp án : B
Hình chữ nhật có các cạnh đối song song và bằng nhau.
Vì ABCD là hình chữ nhật nên \(AB = CD = 6cm\), \(AD = BC = 3,5cm\), cạnh AB và CD song song với nhau, cạnh AD và BC song song với nhau nên chỉ có khẳng định B đúng.
Đáp án B.
-
A.
BD = 10cm.
-
B.
BD = 9cm.
-
C.
BD = 11cm.
-
D.
BD = 12cm.
Đáp án : C
Dựa vào kiến thức về hình vuông: hình vuông có hai đường chéo bằng nhau.
Vì ABCD là hình vuông nên BD = AC = 11 cm.
Đáp án C.
Hình bình hành không có tính chất nào sau đây?
-
A.
Hai cạnh đối song song với nhau.
-
B.
Hai cạnh đối bằng nhau.
-
C.
Bốn cạnh bằng nhau.
-
D.
Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Đáp án : C
Hình bình hành có:
- Hai cặp cạnh đối diện song song và bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Bốn cạnh của hình bình hành không bằng nhau nên khẳng định C sai.
Đáp án C.
Dựa vào kiến thức về cách viết số La Mã.
- Số XIII có 4 thành phần là X, I, I, I tương ứng với các giá trị 10,1,1,1. Do đó biểu diễn số
10 + 1 + 1 + 1 = 13.
- Số 3 được viết là III; số 9 được viết là IX.
a) Sử dụng tính chất phân phối của phép nhân đối với phép cộng.
b) Nếu phép tính có cả cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân chia, cuối cùng đến cộng trừ.
c) Nếu biểu thức có các dấu ngoặc : ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự: \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
a) \(52.26 + 52.74\)
\(\begin{array}{l} = 52.\left( {26 + 74} \right)\\ = 52.100\\ = 5200\end{array}\)
b) \({3^2}.2 - {7^{10}}:{7^9} + {2024^0}\)
\( = 9.2 - {7^1} + 1\)
\( = 18 - 7 + 1\)
\( = 12\)
c) \(107 - \left\{ {38 + \left[ {{{7.3}^2} - 24:6 + {{\left( {9 - 7} \right)}^3}} \right]} \right\}:15\)
\( = \;107 - \{ \;38 + [\;7.9 - 24:6 + {2^3}]\} \;:15\)
\( = 107 - \left\{ {38 + \left[ {63 - 4 + 8} \right]} \right\}:15\)
\( = 107 - \left\{ {38 + 67} \right\}:15\)
\( = 107 - 105:15\)
\( = 107 - 7\)
\( = 100\)
Sử dụng quy tắc chuyển vế kết hợp với các phép tính để tìm x.
a) \(12x - 33 = {3^2}{.3^3}\)
\(12x - 33 = 9.27\;\;\)
\(12x - 33 = \;243\;\;\)
\(12x = 243 + 33\)
\(12x = 276\)
\(x = 276:12\)
\(x = \;23\;\)
Vậy \(x = 23\).
b) \(2\left( {x - 51} \right) = {2.2^3} + 20\)
\(\;2\left( {x - 51} \right) = 16 + 20\)
\(2\left( {x - 51} \right) = 36\)
\(x\; - 51 = 36:2\)
\(x\; - 51 = 18\)
\(\;x = 18 + 51\)
\(x = 69\)
Vậy \(x = 69\).
Tổng số ca-lo còn lại bằng ca–lo hấp thụ cộng ca-lo tiêu hao.
Tổng số ca – lo còn lại sau khi ăn sáng và thực hiện các hoạt động là:
\(290 + 189 + 110 - 70 - 130 = 389\).
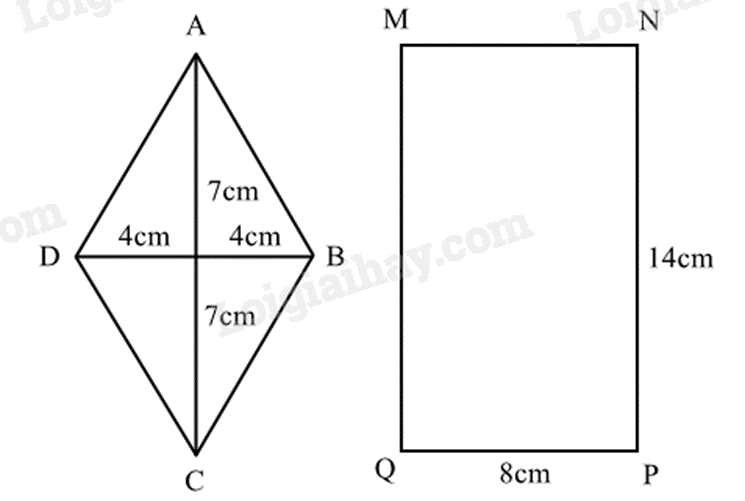
Sử dụng công thức tính diện tích hình chữ nhật, diện tích hình thoi.
Diện tích hình chữ nhật = chiều dài . chiều rộng.
Diện tích hình thoi = \(\frac{1}{2}\). tích hai đường chéo.
a) Độ dài đường chéo AC là:
\(7 + 7 = 14\left( {cm} \right)\)
Độ dài đường chéo BD là:
\(4 + 4 = 8\left( {cm} \right)\)
Diện tích hình thoi ABCD là:
\(\left( {14.8} \right):2 = 56\left( {c{m^2}} \right)\)
Diện tích hình chữ nhật MNPQ là:
\(14.8 = 112\left( {c{m^2}} \right)\)
b) Vì \(56 = 112:2\) nên diện tích của hinh chữ nhật MNPQ gấp đôi diện tích hình thoi ABCD.
Sử dụng tính chất chia hết của một tổng.
Ta có:
\(\begin{array}{l}A = \left( {{{20}^{20}} + {{20}^{21}}} \right) + \left( {{{20}^{22}} + {{20}^{23}}} \right) + ..... + \left( {{{20}^{70}} + {{20}^{71}}} \right)\\ = {20^{20}}\left( {1 + 20} \right) + {20^{22}}\left( {1 + 20} \right) + ..... + {20^{70}}\left( {1 + 20} \right)\\ = 21\left( {{{20}^{20}} + {{20}^{22}} + ... + {{20}^{70}}} \right)\end{array}\)
Vì \(21 \vdots 21\) nên \(21\left( {{{20}^{20}} + {{20}^{22}} + ... + {{20}^{70}}} \right) \vdots 21\) hay \(A \vdots 21\).
Vậy \(A\) chia hết cho 21.