Đề thi khảo sát chất lượng đầu năm Toán 6 Chân trời sáng tạo - Đề số 9
Đề bài

Mua \(6\) quyển vở thì hết \(54000\) đồng. Hỏi mua \(9\) quyển vở như thế thì hết bao nhiêu tiền?
A. \(9000\) đồng
B. \(72000\) đồng
C. \(81000\) đồng
D. \(135000\) đồng

Mai đi từ nhà lúc \(7\) giờ \(15\) phút và đến trường sớm \(8\) phút so với giờ vào học. Lan đi từ nhà lúc \(7\) giờ \(20\) phút và đến trường đúng giờ vào học. Biết giờ vào học là \(8\) giờ. Hỏi Mai và Lan, ai đi từ nhà đến trường mất nhiều thời gian hơn và nhiều hơn bao nhiêu phút?
A. Mai ; \(3\) phút
B. Mai ; \(5\) phút
C. Lan ; \(3\) phút
D. Lan ; \(5\) phút

Một vận động viên đạp xe đạp trên một đường đua là một đường tròn với vận tốc \(25,12\) km/giờ. Anh ta đi trong \(15\) phút thì được một vòng tròn. Tính bán kính đường đua.
A. \(0,25km\)
B. \(0,5km\)
C. \(1km\)
D. \(2km\)
Điền số thích hợp vào ô trống:
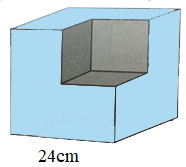
Một khối gỗ dạng hình lập phương có cạnh \(24cm\). Người ta cắt đi một phần gỗ cũng có dạng hình lập phương có cạnh bằng nửa cạnh khối gỗ đó. Mỗi xăng-ti-mét khối gỗ nặng \(0,75\,gam\).
Vậy phần gỗ còn lại nặng
\(kg\).
Điền số thích hợp vào ô trống:
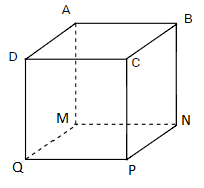
Hình lập phương trên có
cạnh,
mặt.

Người ta làm một cái lồng sắt hình lập phương có độ dài mỗi cạnh là $25dm$. Cứ mỗi mét vuông sắt giá $45000$ đồng. Hỏi người ta làm cái lồng sắt đó hết bao nhiều tiền mua sắt?
A. \(1876500\) đồng
B. \(1768500\) đồng
C. \(1687500\) đồng
D. \(1568700\) đồng

Điền số thích hợp vào ô trống:
Diện tích hình tam giác có độ dài đáy là \(25cm\) và chiều cao là \(16cm\) là
\(c{m^2}.\)
Điền số thích hợp vào ô trống:
Cho hình vẽ như bên dưới:
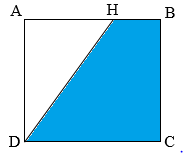
Biết hình vuông \(ABCD\) có diện tích là \(2500d{m^2}\), độ dài cạnh \(AH\) bằng \(70\% \) độ dài đoạn \(AB\).
Vậy diện tích hình thang \(HBCD\) là
\(d{m^2}\).

Lúc \(8\) giờ sáng, người thứ I đi từ A đi qua B để đến C với vận tốc $50$km/giờ. Cùng lúc đó tại B, người thứ II cũng khởi hành và đi cùng chiều với người thứ I với vận tốc $12$km/giờ. Biết rằng khoảng cách AB bằng $19km$. Hỏi hai người gặp nhau lúc mấy giờ?
A. \(0\) giờ \(30\) phút
B. \(8\) giờ \(16\) phút
C. \(8\) giờ \(30\) phút
D. \(9\) giờ \(5\) phút

Điền số thích hợp vào ô trống:
Cho hai số có tổng là \(128\) và hiệu hai số là \(54\).
Vậy số lớn là
, số bé là

Điền số thích hợp vào ô trống để tính bằng cách thuận tiện :
\(45,54 \times 26 + 45,54 + 45,54 \times 73\)
\( = 45,54 \times 26 + 45,54 \times \)
\( + \,45,54 \times 73\)
\( = \)
\( \times \,\,\,(\,26\) +
\(+ 73 ) \)
\( = \)
\(\times (\)
\(+ 73 )\)
\(=\)
\(\times\)
\(=\)

Tìm số trung bình cộng của các số \(12,3;\,\,28,45\) và \(52,31\).
A. \(30,02\)
B. \(31,02\)
C. \(30,12\)
D. \(31,12\)

Chọn dấu thích hợp để điền vào chỗ chấm:
\( 45da{m^2} + 98da{m^2}\;...\;2h{m^2} - 54da{m^2}\)
A. \( < \)
B. \( = \)
C. \( > \)

Điền số thích hợp vào ô trống:
Ba bạn An, Bình, Minh có một số que tính. Số que tính của An bằng $25\% $ tổng số que tính của cả ba bạn. Số que tính của Bình bằng $42\% $ số que tính của cả ba bạn, còn lại là của Minh. Biết số que tính của Minh nhiều hơn số que tính của An là \(24\) que.
Vậy Minh có
que tính.
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
$17,24\xrightarrow{+8,4}$
$\xrightarrow{\times 23}$

Điền số thích hợp vào ô trống:
Viết phân số sau thành số thập phân:
\(\dfrac{{19}}{8} = \)
Lời giải và đáp án

Mua \(6\) quyển vở thì hết \(54000\) đồng. Hỏi mua \(9\) quyển vở như thế thì hết bao nhiêu tiền?
A. \(9000\) đồng
B. \(72000\) đồng
C. \(81000\) đồng
D. \(135000\) đồng
C. \(81000\) đồng
+ Ta thấy càng mua nhiều quyển vở thì càng hết nhiều tiền và ngược lại mua ít quyển vở thì hết ít tiền hơn. Vậy đây là bài toán tỉ lệ thuận.
+ Đối với dạng bài về quan hệ tỉ lệ, ta có thể làm theo 2 cách sau:
Cách 1: dùng phương pháp rút về đơn vị: tính số tiền mua \(1\) quyển vở, sau đó tính số tiền để mua \(1\) quyển vở.
Cách 2: dùng phương pháp tìm tỉ số: số vở tăng lên bao nhiêu lần thì số tiền cũng tăng lên bấy nhiêu lần.
Tóm tắt:
\(6\) quyển vở: \(54000\) đồng
\(9\) quyển vở: … đồng?
Cách 1: Phương pháp rút về đơn vị
Mua \(1\) quyển vở hết số tiền là:
\(54000:6 = 9000\) (đồng)
Mua \(9\) quyển vở như thế hết số tiền là:
\(9000 \times 9 = 81000\) (đồng)
Đáp số: \(81000\) đồng
Cách 2: Phương pháp dùng tỉ số
\(9\) quyển vở gấp \(6\) quyển vở số lần là:
\(9:6 = \dfrac{9}{6} = \dfrac{3}{2}\) (lần)
Mua \(9\) quyển vở như thế hết số tiền là:
\(54000 \times \dfrac{3}{2} = 81000\) (đồng)
Đáp số: \(81000\) đồng

Mai đi từ nhà lúc \(7\) giờ \(15\) phút và đến trường sớm \(8\) phút so với giờ vào học. Lan đi từ nhà lúc \(7\) giờ \(20\) phút và đến trường đúng giờ vào học. Biết giờ vào học là \(8\) giờ. Hỏi Mai và Lan, ai đi từ nhà đến trường mất nhiều thời gian hơn và nhiều hơn bao nhiêu phút?
A. Mai ; \(3\) phút
B. Mai ; \(5\) phút
C. Lan ; \(3\) phút
D. Lan ; \(5\) phút
C. Lan ; \(3\) phút
- Tìm thời gian lúc Mai đi tới trường: Mai đến trường sớm \(8\) phút tức là đến trường lúc \(8\) giờ kém \(8\) phút hay \(7\) giờ \(52\) phút.
- Tính thời gian Mai đi từ nhà đến trường ta lấy thời gian lúc Mai đi tới trường trừ đi thời gian lúc Mai đi từ nhà.
- Tính thời gian Lan đi từ nhà đến trường ta lấy thời gian lúc Lan đi tới trường trừ đi thời gian lúc Lan đi từ nhà.
- So sánh hai kết quả để tìm ai đi mất nhiều thời gian hơn.
- Tìm thời gian đi nhiều hơn ta lấy số đo thời gian lớn hơn trừ đi số đo thời gian bé hơn.
Mai đến trường sớm \(8\) phút tức là đến trường lúc \(8\) giờ kém \(8\) phút hay \(7\) giờ \(52\) phút.
Thời gian Mai đi từ nhà đến trường là:
\(7\) giờ \(52\) phút \( - \,7\) giờ \(15\) phút \( = \,37\) phút
Thời gian Lan đi từ nhà đến trường là:
\(8\) giờ \( - \,7\) giờ \(20\) phút \( = \,40\) phút
Ta có: \(40\) phút \( > \,37\) phút.
Vây Lan đi từ nhà đến trường mất nhiều thời gian hơn và nhiều hơn số thời gian là:
\(\,\,40\) phút \( - \,37\) phút \( = \,3\) phút
Đáp số: Lan ; \(3\) phút.

Một vận động viên đạp xe đạp trên một đường đua là một đường tròn với vận tốc \(25,12\) km/giờ. Anh ta đi trong \(15\) phút thì được một vòng tròn. Tính bán kính đường đua.
A. \(0,25km\)
B. \(0,5km\)
C. \(1km\)
D. \(2km\)
C. \(1km\)
Quãng đường vận động viên đi được trong \(15\) phút chính là chu vi của đường đua hình tròn.
Để giải bài này ta có thể làm như sau:
- Đổi \(15\) phút \( = 0,25\) giờ.
- Tính quãng đường vận động viên đi được khi đạp \(1\) vòng đường đua ta lấy vận tốc nhân với thời gian (\(0,25\) giờ).
- Tính bán kính đường đua ta lấy chu vi chia cho \(3,14\) rồi chia cho \(2\) hoặc chu vi chia cho \(2\) rồi chia cho \(3,14\).
Đổi \(15\) phút \( = \,0,25\) giờ
Quãng đường vận động viên đi được khi đạp \(1\) vòng đường đua là:
\(25,12 \times 0,25 = 6,28\;(km)\)
Vậy chu vi đường đua là \(6,28km\).
Bán kính đường đua là:
\(6,28:3,14:2 = 1\;(km)\)
Đáp số: \(1km\).
Điền số thích hợp vào ô trống:
Một khối gỗ dạng hình lập phương có cạnh \(24cm\). Người ta cắt đi một phần gỗ cũng có dạng hình lập phương có cạnh bằng nửa cạnh khối gỗ đó. Mỗi xăng-ti-mét khối gỗ nặng \(0,75\,gam\).
Vậy phần gỗ còn lại nặng
\(kg\).

Một khối gỗ dạng hình lập phương có cạnh \(24cm\). Người ta cắt đi một phần gỗ cũng có dạng hình lập phương có cạnh bằng nửa cạnh khối gỗ đó. Mỗi xăng-ti-mét khối gỗ nặng \(0,75\,gam\).
Vậy phần gỗ còn lại nặng
\(kg\).

- Tính độ dài cạnh của khối gỗ đã cắt đi (tính \(24:2 = 12cm\)).
- Tính thể tích khối gỗ ban đầu (tính \(24 \times 24 \times 24\)).
- Tính thể tích khối gỗ đã cắt đi (tính \(12 \times 12 \times 12\)).
- Tính thể tích khối gỗ còn lại ta lấy thể tích khối gỗ ban đầu trừ đi thể tích khối gỗ đã cắt đi.
- Tính khối lượng của khối gỗ còn lại ta lấy khối lượng của \(1\) xăng-ti-mét khối gỗ nhân với thể tích khối gỗ còn lại.
Độ dài cạnh của khối gỗ đã cắt đi là:
\(24:2 = 12 \;(cm)\)
Thể tích khối gỗ ban đầu là:
\(24 \times 24 \times 24 = 13824;(c{m^3})\)
Thể tích khối gỗ đã cắt đi là:
\(12 \times 12 \times 12 = 1728 \; (c{m^3})\)
Thể tích khối gỗ còn lại là:
\(13824 - 1728 = 12096 \;(c{m^3})\)
Cân nặng khối gỗ còn lại là:
\(0,75 \times 12096 = 9072\;(g)\)
\(9072g = 9,072kg\)
Đáp số: \(9,072kg\).
Vậy đáp án đúng điền vào ô trống là \(9,072\).
Điền số thích hợp vào ô trống:

Hình lập phương trên có
cạnh,
mặt.
Hình lập phương trên có
cạnh,
mặt.
- Hình lập phương đã cho có \(12\) cạnh là: cạnh \(AB\), cạnh \(BC\), cạnh \(CD\), cạnh \(DA\), cạnh \(MN\), cạnh \(NP\), cạnh \(PQ\), cạnh \(MQ\), cạnh \(AM\), cạnh \(BN\), cạnh \(CP\), cạnh \(DQ\).
- Hình lập phương đã cho có \(6\) mặt là: mặt \(ABCD\), mặt \(MNPQ\) mặt \(ABNM\), mặt \(DCPQ\), mặt \(DAMQ\), mặt \(CBNP\).
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(12;\,\,6\).

Người ta làm một cái lồng sắt hình lập phương có độ dài mỗi cạnh là $25dm$. Cứ mỗi mét vuông sắt giá $45000$ đồng. Hỏi người ta làm cái lồng sắt đó hết bao nhiều tiền mua sắt?
A. \(1876500\) đồng
B. \(1768500\) đồng
C. \(1687500\) đồng
D. \(1568700\) đồng
C. \(1687500\) đồng
Vì cái lồng sắt đó hình lập phương nên diện tích sắt phải mua bằng diện tích toàn phần của hình lập phương có cạnh $25dm.$
Để giải bài này ta có thể thực hiện như sau:
- Đổi đơn vị đo độ dài của mỗi cạnh về đơn vị là mét.
- Tính diện tích mỗi mặt của lồng sắt đó ta lấy độ dài mỗi cạnh của lồng sắt đó nhân với chính nó.
- Tính diện tích sắt cần phải mua để làm cái lồng đó ta lấy diện tích một mặt của lồng sắt đó nhân với \(6\).
- Tính số tiền cần dùng để mua sắt ta lấy giá tiền mua mỗi mét vuông sắt nhân với diện tích sắt cần phải mua.
Đổi \(25dm = 2,5m\).
Diện tích một mặt của cái lồng sắt đó là:
\(2,5 \times 2,5 = 6,25 \;({m^2})\)
Diện tích sắt dùng để làm cái lồng đó là:
\(6,25 \times 6 = 37,5 \;({m^2})\)
Số tiền cần dùng để mua sắt làm cái lồng đó là:
\(45000 \times 37,5 = 1687500\) (đồng)
Đáp số: \(1687500\) đồng.

Điền số thích hợp vào ô trống:
Diện tích hình tam giác có độ dài đáy là \(25cm\) và chiều cao là \(16cm\) là
\(c{m^2}.\)
Diện tích hình tam giác có độ dài đáy là \(25cm\) và chiều cao là \(16cm\) là
\(c{m^2}.\)
Độ dài đáy và chiều cao đã có cùng đơn vị đo nên để tính diện tích ta lấy độ dài đáy nhân với chiều cao rồi chia cho \(2\).
Diện tích tam giác đó là:
\(\dfrac{{25 \times 16}}{2} = 200\left( {c{m^2}} \right)\)
Đáp số: \(200c{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(200\).
Điền số thích hợp vào ô trống:
Cho hình vẽ như bên dưới:

Biết hình vuông \(ABCD\) có diện tích là \(2500d{m^2}\), độ dài cạnh \(AH\) bằng \(70\% \) độ dài đoạn \(AB\).
Vậy diện tích hình thang \(HBCD\) là
\(d{m^2}\).
Cho hình vẽ như bên dưới:

Biết hình vuông \(ABCD\) có diện tích là \(2500d{m^2}\), độ dài cạnh \(AH\) bằng \(70\% \) độ dài đoạn \(AB\).
Vậy diện tích hình thang \(HBCD\) là
\(d{m^2}\).
- Tìm độ dài cạnh hình vuông.
- Tìm độ dài các cạnh đáy và chiều cao của hình thang sau đó để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho \(2\).
Ta có \(50 \times 50 = 2500\). Vậy độ dài cạnh hình vuông \(ABCD\) là \(50dm\) hay \(AB = BC = CD = AD = 50dm\).
Ta có \(HBCD\) là hình thang vuông với chiều cao là cạnh \(BC\), hai đáy là \(HB,\,\,DC\).
Độ dài cạnh \(AH\) là:
\(50:100 \times 70 = 35\;(dm)\)
Độ dài cạnh \(HB\) là:
\(50 - 35 = 15\;(dm)\)
Diện tích hình thang \(HBCD\) là:
\((15 + 50) \times 50:2 = 1625\;(d{m^2})\)
Đáp số: \(1625d{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(1625\).

Lúc \(8\) giờ sáng, người thứ I đi từ A đi qua B để đến C với vận tốc $50$km/giờ. Cùng lúc đó tại B, người thứ II cũng khởi hành và đi cùng chiều với người thứ I với vận tốc $12$km/giờ. Biết rằng khoảng cách AB bằng $19km$. Hỏi hai người gặp nhau lúc mấy giờ?
A. \(0\) giờ \(30\) phút
B. \(8\) giờ \(16\) phút
C. \(8\) giờ \(30\) phút
D. \(9\) giờ \(5\) phút
C. \(8\) giờ \(30\) phút
Theo đề bài, hai người xuất phát cùng lúc. Để giải bài này ta làm như sau:
- Tính hiệu vận tốc của hai người.
- Thời gian đi để gặp nhau bằng khoảng cách ban đầu giữa hai người chia cho hiệu hai vận tốc.
- Đổi số đo thời gian dạng số thập phân sang dạng số tự nhiên.
- Thời gian lúc hai người gặp nhau = thời gian xuất phát + thời gian đi để gặp nhau.
Hiệu vận tốc của hai người là:
\(50 - 12 = 38\) (km/giờ)
Thời gian đi để hai người gặp nhau là:
\(19:38 = 0,5\) (giờ)
Đổi: \(0,5\) giờ \( = \,\,30\) phút
Hai người gặp nhau lúc:
\(8\) giờ \( + \,\,30\) phút \( = \,\,8\) giờ \(30\) phút
Đáp số: \(8\) giờ \(30\) phút

Điền số thích hợp vào ô trống:
Cho hai số có tổng là \(128\) và hiệu hai số là \(54\).
Vậy số lớn là
, số bé là
Cho hai số có tổng là \(128\) và hiệu hai số là \(54\).
Vậy số lớn là
, số bé là
Đây là dạng toán tìm hai số khi biết tổng và hiệu của \(2\) số đó.
Để tìm hai số ta áp dụng công thức sau:
Số bé = (tổng – hiệu) : \(2\);
Số lớn = (tổng + hiệu) : \(2\).
Ta có sơ đồ:
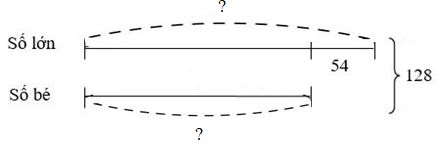
Số lớn là : \((128 + 54):\,2 = 91\)
Số bé là: \(128 - 91 = 37\)
Đáp số: Số bé: \(37\);
Số lớn: \(91\).
Vậy hai số điền vào ô trống theo thứ tự là \(91;\,37\).

Điền số thích hợp vào ô trống để tính bằng cách thuận tiện :
\(45,54 \times 26 + 45,54 + 45,54 \times 73\)
\( = 45,54 \times 26 + 45,54 \times \)
\( + \,45,54 \times 73\)
\( = \)
\( \times \,\,\,(\,26\) +
\(+ 73 ) \)
\( = \)
\(\times (\)
\(+ 73 )\)
\(=\)
\(\times\)
\(=\)
\(45,54 \times 26 + 45,54 + 45,54 \times 73\)
\( = 45,54 \times 26 + 45,54 \times \)
\( + \,45,54 \times 73\)
\( = \)
\( \times \,\,\,(\,26\) +
\(+ 73 ) \)
\( = \)
\(\times (\)
\(+ 73 )\)
\(=\)
\(\times\)
\(=\)
Áp dụng công thức \(a \times b + a + a \times c = a \times b + a \times 1 + a \times c = a \times (b + 1 + c)\)
\(\begin{array}{l}45,54 \times 26 + 45,54 + 45,54 \times 73\\ = 45,54 \times 26 + 45,54 \times 1 + 45,54 \times 73\\ = 45,54 \times (26 + 1 + 73)\\ = 45,54 \times 100\\ = 4554\end{array}\)
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trên xuống dưới, từ trái sang phải là \(1\,;\,\,45,54\,;\,\,1\,;\,\,45,54\,;\,\,27\,;\,\,45,54\,;\,\,100\,;\,\,4554\).

Tìm số trung bình cộng của các số \(12,3;\,\,28,45\) và \(52,31\).
A. \(30,02\)
B. \(31,02\)
C. \(30,12\)
D. \(31,12\)
B. \(31,02\)
Muốn tìm số trung bình cộng của nhiều số, trước hết ta tìm tổng của các số đó rồi lấy tổng đó chia cho số các số hạng.
Ta thấy có tất cả 3 số.
Vậy số trung bình cộng của các số \(12,3;\,\,28,45\) và \(52,31\) là:
\((12,3+28,45+52,31) : 3 = 31,02\)
Đáp số: \(31,02\).

Chọn dấu thích hợp để điền vào chỗ chấm:
\( 45da{m^2} + 98da{m^2}\;...\;2h{m^2} - 54da{m^2}\)
A. \( < \)
B. \( = \)
C. \( > \)
A. \( < \)
- Muốn so sánh được hai vế trước tiên ta phải tính giá trị của cả hai vế và đưa về cùng đơn vị \(da{m^2}\).
- Áp dụng quy tắc đổi đơn vị diện tích từ đơn vị lớn sang đơn vị bé: \(1hm^2=100dam^2\).
Ta có \(45da{m^2} + 98da{m^2} \)\(= 143da{m^2} \)
Lại có \(2h{m^2}= 200da{m^2} \)\(\Rightarrow 2h{m^2} - 54da{m^2} \)\(= 200da{m^2} - 54da{m^2} \)\(= 146da{m^2}\)
Vì \(143da{m^2} < 146da{m^2}\)
nên \(45da{m^2} + 98da{m^2} \)\(< 2h{m^2} - 54da{m^2}\) .
Vậy dấu cần điền là \( < \) .

Điền số thích hợp vào ô trống:
Ba bạn An, Bình, Minh có một số que tính. Số que tính của An bằng $25\% $ tổng số que tính của cả ba bạn. Số que tính của Bình bằng $42\% $ số que tính của cả ba bạn, còn lại là của Minh. Biết số que tính của Minh nhiều hơn số que tính của An là \(24\) que.
Vậy Minh có
que tính.
Ba bạn An, Bình, Minh có một số que tính. Số que tính của An bằng $25\% $ tổng số que tính của cả ba bạn. Số que tính của Bình bằng $42\% $ số que tính của cả ba bạn, còn lại là của Minh. Biết số que tính của Minh nhiều hơn số que tính của An là \(24\) que.
Vậy Minh có
que tính.
Coi tổng số que tính của cả ba bạn là \(100\% \).
- Tính tỉ số phần trăm số que tính của Minh và tổng số que tính, ta lấy \(100\% - 25\% - 42\% = 33\% \).
- Tính hiệu tỉ số phần trăm giữa số que tính của Minh và An, ta lấy \(33\% - 25\% = 8\% \).
- Khi đó \(8\% \) tổng số que tính chính là \(24\). Để tính tổng số que tính ta lấy \(24\) chia cho \(8\) rồi nhân với \(100\) .
- Tính số que tính của Minh ta lấy tổng số que tính chia cho \(100\) rồi nhân với \(33\).
Số que tính của Minh chiếm số phần trăm so với tổng số que tính của ba bạn là:
\(100\% - 25\% - 42\% = 33\% \)
Số que tính của Minh nhiều hơn số que tính của An số phần trăm là:
\(33\% - 25\% = 8\% \)
Ba bạn có tất cả số que tính là:
\(24:8 \times 100 = 300\) (que tính)
Minh có số que tính là:
\(300:100 \times 33 = 99\) (que tính)
Đáp số: \(99\) que tính.
Vậy đáp án đúng điền vào ô trống là \(99\).
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
$17,24\xrightarrow{+8,4}$
$\xrightarrow{\times 23}$
$17,24\xrightarrow{+8,4}$
$\xrightarrow{\times 23}$
Tính lần lượt từ trái sang phải.
Tính lần lượt từ trái sang phải ta có:
\(\begin{array}{l}17,24 + 8,4 = 25,64\\25,64 \times 23 = 589,72\end{array}\)
Vậy đáp án đúng điền vào ô trống thep thứ tự từ trái sang phải là \(25,64\,;\,\,589,72\).

Điền số thích hợp vào ô trống:
Viết phân số sau thành số thập phân:
\(\dfrac{{19}}{8} = \)
Viết phân số sau thành số thập phân:
\(\dfrac{{19}}{8} = \)
- Viết phân số đã cho thành phân số thập phân bằng cách nhân cả tử số và mẫu số của phân số đã cho với một số thích hợp để có mẫu số là $10;{\rm{ }}100;{\rm{ }}1000...$
- Viết phân số thập phân vừa viết được thành số thập phân gọn nhất.
Ta có: \(\dfrac{{19}}{8} \)\(= \dfrac{{19 \times 125}}{{8 \times 125}} \)\(= \dfrac{{2375}}{{1000}}\)\( = 2,375\)
Vậy đáp án cần điền vào ô trống là \(2,375.\)