Đề thi khảo sát chất lượng đầu năm Toán 6 Chân trời sáng tạo - Đề số 6
Đề bài

Tính: \(23,2\,:\,1,45\).
A. \(1,6\)
B. \(1,8\)
C. \(16\)
D. \(18\)

Một hình lập phương có cạnh \(2cm\). Nếu gấp cạnh của hình lập phương lên \(3\) lần thì diện tích xung quanh và diện tích toàn phần tăng số lần lần lượt là:
A. \(3\) lần; \(3\) lần
B. \(6\) lần; \(9\) lần
C. \(4\) lần; \(6\) lần
D. \(9\) lần; \(9\) lần

Điền số thích hợp vào ô trống:
Lúc \(7\) giờ \(40\) phút ca nô đi ngược dòng từ bến B và về bến A lúc \(8\) giờ \(20\) phút. Biết vận tốc của ca nô khi nước lặng là \(27\) km/giờ và vận tốc dòng nước là \(3\) km/giờ.
Vậy khoảng cách giữa hai bến A và bến B là
\(km\).
Cho hình vẽ như sau:
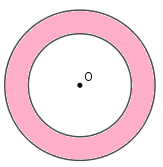
Biết hai hình tròn có cùng tâm \(O\) ta có bán kính lần lượt là \(5dm\) và \(7,5dm\).
Vậy diện tích phần đã tô màu của hình tròn là:
A. \(490,625d{m^2}\)
B. \(255,125d{m^2}\)
C. \(176,625d{m^2}\)
D. \(98,125d{m^2}\)
 Cho tam giác \(ABC\) có $BC = 67dm$. Nếu kéo dài đoạn \(BC\) thêm một đoạn \(CD = 15dm\) thì diện tích tam giác tăng thêm $255d{m^2}$ . Tính diện tích tam giác \(ABC\).
Cho tam giác \(ABC\) có $BC = 67dm$. Nếu kéo dài đoạn \(BC\) thêm một đoạn \(CD = 15dm\) thì diện tích tam giác tăng thêm $255d{m^2}$ . Tính diện tích tam giác \(ABC\).
A. \(569,5d{m^2}\)
B. \(1139d{m^2}\)
C. \(1394d{m^2}\)
D. \(2278d{m^2}\)

Một thửa ruộng hình thang có đáy bé bằng \(\dfrac{3}{5}\) đáy lớn, chiều cao bằng $\dfrac{1}{4}$ đáy lớn. Biết đáy lớn hình thang là $260m$. Để làm sạch cỏ trên thửa ruộng, bác Hùng cần $0,75$ giờ cho mỗi $100{m^2}$ đất. Hỏi bác Hùng cần dùng bao nhiêu giờ để làm sạch cỏ trên cả thửa ruộng ấy?
A. \(76,05\) giờ
B. \(101,4\) giờ
C. \(180\) giờ
D. \(202,8\) giờ
 Nối câu mô tả hình dạng với hình tam giác tương ứng:
Nối câu mô tả hình dạng với hình tam giác tương ứng:
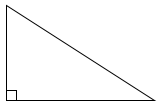
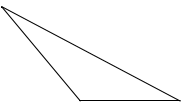
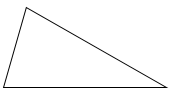
Hình tam giác có ba góc nhọn.
Hình tam giác có một góc vuông
và hai góc nhọn
Hình tam giác có một góc tù
và hai góc nhọn.

Một con rái cá có thể bơi với vận tốc \(25,2\) km/giờ. Một con ngựa chạy với vận tốc \(5,5\) m/giây. Hỏi trong \(1\) phút, con nào di chuyển được quãng đường dài hơn và dài hơn bao nhiêu mét?
A. Con rái cá; \(9m\)
B. Con rái cá; \(90m\)
C. Con ngựa; \(9m\)
D. Con ngựa; \(90m\)

Một tấm vải dài 60m, người ta đã dùng $\frac{3}{4}$ tấm vải đó để may quần áo. Số vải còn lại người ta đem may các túi, mỗi túi hết $\frac{4}{5}m$vải. Hỏi may được tất cả bao nhiêu cái túi như vậy?
-
A.
20 túi
-
B.
15 túi
-
C.
30 túi
-
D.
40 túi

Điền số thích hợp vào ô trống:
Bác Lan mang trứng ra chợ bán. Buổi sáng bác bán được $25\% $ tổng số trứng, buổi chiều bác bán được $32,5\% $ tổng số trứng thì bác Lan còn lại \(102\) quả trứng.
Vậy buổi sáng bác Lan đã bán được
quả trứng.

Hỗn số “mười ba và hai mươi lăm phần ba mươi tám” được viết là
A. \(3\dfrac{{25}}{8}\)
B. \(13\dfrac{{25}}{{38}}\)
C. \(30\dfrac{5}{{38}}\)
D. \(31\dfrac{{25}}{{38}}\)

So sánh \(x\) và \(y\) biết rằng:
\(y - \left( {\dfrac{4}{{15}} + \dfrac{1}{5}} \right):\dfrac{4}{9} = \dfrac{5}{8};\)
\(\left( {x + \dfrac{5}{6}} \right) \times \dfrac{{12}}{{25}} = \dfrac{{47}}{{50}}\)
A. \(x > y\)
B. \(x < y\)
C. \(x = y\)

Tìm \(x\) biết: \(x - 4,5 = 7,98\)
A. \(x = 52,98\)
B. \(x = 84,3\)
C. \(x = 8,43\)
D. \(x = 12,48\)

Cho \(4da{m^2} = \) $...$ \(d{m^2}\) .
Số thích hợp điền vào chỗ trống là:
A.\(40\)
B. \(400\)
C. \(4000\)
D. \(40000\)

$316 - 15,74 \times \;8 $ $ ...$ $18,45 \times 7 + 60,93$
Dấu thích hợp điền vào chỗ chấm là:
A. \( = \)
B. \( > \)
C. \( < \)
Lời giải và đáp án

Tính: \(23,2\,:\,1,45\).
A. \(1,6\)
B. \(1,8\)
C. \(16\)
D. \(18\)
C. \(16\)
- Phần thập phân của số \(1,45\) có hai chữ số.
- Chuyển dấu phẩy của số \(23,2\) sang bên phải hai chữ số, tuy nhiên phần thập phân của số \(23,2\) chỉ có một chữ số nên coi \(23,2 = 23,20\), chuyển dấu phẩy sang hai chữ số được \(2320\); bỏ dấu phẩy ở số \(1,45\) được \(145\).
- Thực hiện phép chia \(2320:145\).
Đặt tính và thực hiện tính ta có:
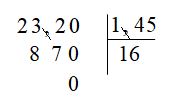
Vậy \(23,2:1,45 = 16\).

Một hình lập phương có cạnh \(2cm\). Nếu gấp cạnh của hình lập phương lên \(3\) lần thì diện tích xung quanh và diện tích toàn phần tăng số lần lần lượt là:
A. \(3\) lần; \(3\) lần
B. \(6\) lần; \(9\) lần
C. \(4\) lần; \(6\) lần
D. \(9\) lần; \(9\) lần
D. \(9\) lần; \(9\) lần
- Tính độ dài cạnh hình lập phương mới : \(2 \times 3 = 6cm\).
- Tính diện xung quanh và diện tích toàn phần của hình lập phương cạnh \(2cm\).
- Tính diện xung quanh và diện tích toàn phần của hình lập phương cạnh \(6cm\).
- Tính xem diện tích xung quanh của hình lập phương cạnh \(6cm\) gấp bao nhiêu lần diện tích xung quanh của hình lập phương cạnh \(2cm\) ta lấy diện tích xung quanh của hình lập phương cạnh \(6cm\) chia cho diện tích xung quanh của hình lập phương cạnh \(2cm\).
- Làm tương tự để tìm diện tích toàn phần của hình lập phương cạnh \(6cm\) gấp bao nhiêu lần diện tích toàn phần của hình lập phương cạnh \(2cm\).
Độ dài cạnh hình lập phương khi gấp lên \(3\) lần là:
\(2 \times 3 = 6\;(cm)\)
Diện tích một mặt của hình lập phương cạnh \(2cm\) là:
\(2 \times 2 = 4\;(c{m^2})\)
Diện tích xung quanh của hình lập phương cạnh \(2cm\) là:
\(4 \times 4 = 16\;(c{m^2})\)
Diện tích toàn phần của hình lập phương cạnh \(2cm\) là:
\(4 \times 6 = 24\;(c{m^2})\)
Diện tích một mặt của hình lập phương cạnh \(6cm\) là:
\(6 \times 6 = 36\;(c{m^2})\)
Diện tích xung quanh của hình lập phương cạnh \(6cm\) là:
\(36 \times 4 = 144\;(c{m^2})\)
Diện tích toàn phần của hình lập phương cạnh \(6cm\) là:
\(36 \times 6 = 216\;(c{m^2})\)
Diện tích xung quanh của hình lập phương cạnh \(6cm\) gấp diện tích xung quanh của hình lập phương cạnh \(2cm\) số lần là:
\(144:16 = 9\) (lần)
Diện tích toàn phần của hình lập phương cạnh \(6cm\) gấp diện tích toàn phần của hình lập phương cạnh \(2cm\) số lần là:
\(216:24 = 9\) (lần)
Vậy nếu gấp cạnh của hình lập phương lên \(3\) lần thì diện tích xung quanh và diện tích toàn phần đều tăng lên \(9\) lần.

Điền số thích hợp vào ô trống:
Lúc \(7\) giờ \(40\) phút ca nô đi ngược dòng từ bến B và về bến A lúc \(8\) giờ \(20\) phút. Biết vận tốc của ca nô khi nước lặng là \(27\) km/giờ và vận tốc dòng nước là \(3\) km/giờ.
Vậy khoảng cách giữa hai bến A và bến B là
\(km\).
Lúc \(7\) giờ \(40\) phút ca nô đi ngược dòng từ bến B và về bến A lúc \(8\) giờ \(20\) phút. Biết vận tốc của ca nô khi nước lặng là \(27\) km/giờ và vận tốc dòng nước là \(3\) km/giờ.
Vậy khoảng cách giữa hai bến A và bến B là
\(km\).
- Vận tốc ngược dòng \( = \) vận tốc khi nước yên lặng \( - \) vận tốc dòng nước.
- Tính thời gian đi ngược dòng từ bến B về bến A ta lấy thời gian lúc về đến bến A trừ đi thời gian lúc đi từ bến B.
- Quãng đường \( = \) vận tốc ngược dòng \( \times \) thời gian đi ngược dòng.
Vận tốc của ca nô khi đi ngược dòng là:
\(27 - 3 = 24\) (km/giờ)
Ca nô đi từ bến B về bến A hết số thời gian là:
\(8\) giờ \(20\) phút \( - \,7\) giờ \(40\) phút \( = \,40\) phút
Đổi \(40\) phút \( = \dfrac{2}{3}\) giờ
Khoảng cách giữa hai bến A và bến B là:
\(24 \times \dfrac{2}{3} = 16 \;(km)\)
Đáp số: $16 km$.
Vậy đáp án đúng điền vào ô trống là \(16\).
Cho hình vẽ như sau:

Biết hai hình tròn có cùng tâm \(O\) ta có bán kính lần lượt là \(5dm\) và \(7,5dm\).
Vậy diện tích phần đã tô màu của hình tròn là:
A. \(490,625d{m^2}\)
B. \(255,125d{m^2}\)
C. \(176,625d{m^2}\)
D. \(98,125d{m^2}\)
D. \(98,125d{m^2}\)
Tính diện tích hình tròn bán kính \(5dm\) và \(7,5dm\). Diện tích phần tô màu bằng hiệu diện tích giữa hai hình tròn.
Diện tích hình tròn tâm \(O\) bán kính \(7,5dm\) là:
\(7,5 \times 7,5 \times 3,14 = 176,625\;(d{m^2})\)
Diện tích hình tròn tâm \(O\) bán kính \(5dm\) là:
\(5 \times 5 \times 3,14 = 78,5\;(d{m^2})\)
Diện tích phần đã tô màu của hình tròn là :
\(176,625 - 78,5 = 98,125\;(d{m^2})\)
Đáp số: \(98,125d{m^2}\).
 Cho tam giác \(ABC\) có $BC = 67dm$. Nếu kéo dài đoạn \(BC\) thêm một đoạn \(CD = 15dm\) thì diện tích tam giác tăng thêm $255d{m^2}$ . Tính diện tích tam giác \(ABC\).
Cho tam giác \(ABC\) có $BC = 67dm$. Nếu kéo dài đoạn \(BC\) thêm một đoạn \(CD = 15dm\) thì diện tích tam giác tăng thêm $255d{m^2}$ . Tính diện tích tam giác \(ABC\).
A. \(569,5d{m^2}\)
B. \(1139d{m^2}\)
C. \(1394d{m^2}\)
D. \(2278d{m^2}\)
B. \(1139d{m^2}\)
- Vẽ hình theo đề bài ta thấy diện tích phần tăng thêm là diện tích tam giác \(ACD\) có đáy \(CD = 15cm\) và chiều cao chính là chiều cao \(AH\) của tam giác \(ABC\), từ đó áp dụng công thức \(h = S \times 2:a\) ta tìm được chiều cao \(AH\).
- Tính diện tích tam giác \(ABC\) theo công thức \(S = a \times h:2\).
Theo bài ra ta có hình vẽ

Phần diện tích tăng thêm chính là diện tích của hình tam giác có đáy là $15dm$ và chiều cao cũng chính là chiều cao \(AH\) của tam giác \(ABC\).
Chiều cao của tam giác \(ABC\) là:
\(255 \times 2:15 = 34\;(dm)\)
Diện tích tam giác \(ABC\) là
\(67 \times 34:2 = 1139\left( {d{m^2}} \right)\)
Đáp số: \(1139d{m^2}\).

Một thửa ruộng hình thang có đáy bé bằng \(\dfrac{3}{5}\) đáy lớn, chiều cao bằng $\dfrac{1}{4}$ đáy lớn. Biết đáy lớn hình thang là $260m$. Để làm sạch cỏ trên thửa ruộng, bác Hùng cần $0,75$ giờ cho mỗi $100{m^2}$ đất. Hỏi bác Hùng cần dùng bao nhiêu giờ để làm sạch cỏ trên cả thửa ruộng ấy?
A. \(76,05\) giờ
B. \(101,4\) giờ
C. \(180\) giờ
D. \(202,8\) giờ
B. \(101,4\) giờ
- Tìm đáy lớn và chiều cao theo quy tắc: muốn tìm phân số của một số ta lấy số đó nhân với phân số.
- Tìm diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).
- Tìm số giờ để làm sạch cỏ theo bài toán tỉ lệ thuận: tìm tỉ số giữa diện tích và \(100m^2\), diện tích gấp \(100m^2\) bao nhiêu lần thì số giờ để làm sạch cỏ cũng gấp \(0,75\) giờ bấy nhiêu lần.
Độ dài đáy bé của thửa ruộng đó là:
$260 \times \dfrac{3}{5} = 156\;(m)$
Chiều cao của thửa ruộng đó là:
$260 \times \dfrac{1}{4} = 65\;(m)$
Diện tích của thửa ruộng đó là:
$\dfrac{{(156 + 260) \times 65}}{2} = 13520\;({m^2})$
$13520{m^2}$ gấp $100{m^2}$ số lần là:
$13520:100 = 135,2$ (lần)
Bác Hùng cần dùng số giờ để làm sạch cỏ trên cả thửa ruộng đó là:
\(0,75 \times 135,2 = 101,4\) (giờ)
Đáp số: \(101,4\) giờ.
 Nối câu mô tả hình dạng với hình tam giác tương ứng:
Nối câu mô tả hình dạng với hình tam giác tương ứng:



Hình tam giác có ba góc nhọn.
Hình tam giác có một góc vuông
và hai góc nhọn
Hình tam giác có một góc tù
và hai góc nhọn.

Hình tam giác có một góc vuông
và hai góc nhọn

Hình tam giác có một góc tù
và hai góc nhọn.

Hình tam giác có ba góc nhọn.
Quan sát các góc trong một tam giác để mô ta tam giác đã cho.
Quan sát các tam giác theo thứ tự từ trên xuống dưới ta có:
- Hình tam giác thứ nhất có một góc vuông và hai góc nhọn
- Hình tam giác thứ hai có một góc tù và hai góc nhọn.
- Hình tam giác thứ ba có ba góc nhọn.

Một con rái cá có thể bơi với vận tốc \(25,2\) km/giờ. Một con ngựa chạy với vận tốc \(5,5\) m/giây. Hỏi trong \(1\) phút, con nào di chuyển được quãng đường dài hơn và dài hơn bao nhiêu mét?
A. Con rái cá; \(9m\)
B. Con rái cá; \(90m\)
C. Con ngựa; \(9m\)
D. Con ngựa; \(90m\)
B. Con rái cá; \(90m\)
- Đổi \(1\) phút \( = \,\dfrac{1}{{60}}\) giờ, tính độ dài quãng đường con rái cá bơi được theo đơn vị là ki-lô-mét bằng cách lấy vận tốc nhân với thời gian.
- Đổi kết quả vừa tìm được sang đơn vị là mét.
- Đổi \(1\) phút \( = 60\) giây, tính độ dài quãng đường con ngựa chạy được theo đơn vị là mét bằng cách lấy vận tốc nhân với thời gian.
- So sánh kết quả để tìm con nào di chuyển được quãng đường dài hơn.
- Tính quãng đường dài hơn bao nhiêu ki-lô-mét ta lấy quãng đường dài hơn trừ quãng đường ngắn hơn.
Đổi: \(1\) phút \( = \dfrac{1}{{60}}\) giờ; \(1\) phút \( = 60\) giây.
Quãng đường con rái cá bơi được trong \(1\) phút là:
\(25,2 \times \dfrac{1}{{60}} = 0,42\;(km)\)
Đổi: \(0,42km = 420m\)
Quãng đường con ngựa chạy được trong \(1\) phút là:
\(5,5 \times 60 = 330\;(m)\)
Ta có: \(420m > 330m\)
Vậy trong \(1\) phút con rái cá di chuyển được quãng đường dài hơn và dài hơn số mét là:
\(420m - 330m = 90\;(m)\)
Đáp số: Con rái cá; \(90m\).

Một tấm vải dài 60m, người ta đã dùng $\frac{3}{4}$ tấm vải đó để may quần áo. Số vải còn lại người ta đem may các túi, mỗi túi hết $\frac{4}{5}m$vải. Hỏi may được tất cả bao nhiêu cái túi như vậy?
-
A.
20 túi
-
B.
15 túi
-
C.
30 túi
-
D.
40 túi
Đáp án : A
- Tính số vải dùng để may quần áo ta lấy tổng số mét vải nhân với $\frac{3}{4}$.
- Tính số vải dùng để may túi ta lấy tổng số mét vải trừ đi số vải dùng để may quần áo.
- Tìm số túi được may ta lấy số vải dùng để may túi chia cho số mét vải để may $1$ cái túi.
Người ta may quần áo hết số mét vải là:
$60 \times \frac{3}{4} = 45{\mkern 1mu} {\mkern 1mu} (m)$
Số vải dùng để may túi là:
$60 - 45{\mkern 1mu} = 15{\mkern 1mu} (m)$
May được tất cả số cái túi là:
$15:\frac{3}{4} = 20$ (cái)
Đáp số: 20 cái.

Điền số thích hợp vào ô trống:
Bác Lan mang trứng ra chợ bán. Buổi sáng bác bán được $25\% $ tổng số trứng, buổi chiều bác bán được $32,5\% $ tổng số trứng thì bác Lan còn lại \(102\) quả trứng.
Vậy buổi sáng bác Lan đã bán được
quả trứng.
Bác Lan mang trứng ra chợ bán. Buổi sáng bác bán được $25\% $ tổng số trứng, buổi chiều bác bán được $32,5\% $ tổng số trứng thì bác Lan còn lại \(102\) quả trứng.
Vậy buổi sáng bác Lan đã bán được
quả trứng.
Muốn biết buổi sáng bác Lan bán được bao nhiêu quả trứng ta cần tính được tổng số quả trứng bác mang đi chợ bán.
- Coi số trứng bác Lan mang đi chợ là \(100\% \). Số trứng còn lại sẽ chiếm \(100\% - 25\% - 32,5\% = 42,5\% \) tổng số trứng.
- Khi đó \(42,5\% \) tổng số trứng là \(102\) quả trứng. Để tìm tổng số trứng ta lấy \(102\) chia cho \(42,5\) rồi nhân với \(100\).
- Tìm số trứng đã bán buổi sáng ta lấy tổng số trứng chia cho \(100\) rồi nhân với \(25\).
Số trứng còn lại chiếm số phần trăm so với tổng số trứng là:
\(100\% - 25\% - 32,5\% = 42,5\% \)
Tổng số quả trứng bác Lan mang đi chợ bán là:
\(102:42,5 \times 100 = 240\) (quả)
Buổi sáng bác Lan bán được số quả trứng là:
\(240:100 \times 25 = 60\) (quả)
Đáp số: \(60\) quả.
Vậy đáp án đúng điền vào ô trống là \(60\).

Hỗn số “mười ba và hai mươi lăm phần ba mươi tám” được viết là
A. \(3\dfrac{{25}}{8}\)
B. \(13\dfrac{{25}}{{38}}\)
C. \(30\dfrac{5}{{38}}\)
D. \(31\dfrac{{25}}{{38}}\)
B. \(13\dfrac{{25}}{{38}}\)
Khi viết hỗn số, ta viết phần nguyên rồi mới viết phần phân số.
Hỗn số “mười ba và hai mươi lăm phần ba mươi tám” được viết là \(13\dfrac{{25}}{{38}}\).

So sánh \(x\) và \(y\) biết rằng:
\(y - \left( {\dfrac{4}{{15}} + \dfrac{1}{5}} \right):\dfrac{4}{9} = \dfrac{5}{8};\)
\(\left( {x + \dfrac{5}{6}} \right) \times \dfrac{{12}}{{25}} = \dfrac{{47}}{{50}}\)
A. \(x > y\)
B. \(x < y\)
C. \(x = y\)
B. \(x < y\)
Tìm \(x;\,\,y\) sau đó so sánh hai số đó.
Ta có:
$y - \left( {\dfrac{4}{{15}} + \dfrac{1}{5}} \right):\dfrac{4}{9} = \dfrac{5}{8}$
$y - \dfrac{7}{{15}}:\dfrac{4}{9} = \dfrac{5}{8}$
$y - \dfrac{7}{{15}} \times \dfrac{9}{4} = \dfrac{5}{8}$
$y - \dfrac{{21}}{{20}} = \dfrac{5}{8}$
$y = \dfrac{5}{8} + \dfrac{{21}}{{20}}$
$y = \dfrac{{67}}{{40}}$
+ Lại có
$\left( {x + \dfrac{5}{6}} \right) \times \dfrac{{12}}{{25}} = \dfrac{{47}}{{50}}$
$x + \dfrac{5}{6} = \dfrac{{47}}{{50}}:\dfrac{{12}}{{25}}$
$x + \dfrac{5}{6} = \dfrac{{47}}{{50}} \times \dfrac{{25}}{{12}}$
$x + \dfrac{5}{6} = \dfrac{{47}}{{24}}$
$x = \dfrac{{47}}{{24}} - \dfrac{5}{6}$
$x = \dfrac{9}{8}$
Ta có: \(\dfrac{9}{8} = \dfrac{{9 \times 5}}{{8 \times 5}} = \dfrac{{45}}{{40}}\)
Vì \(\dfrac{{67}}{{40}} > \dfrac{{45}}{{40}}\) nên \(\dfrac{{67}}{{40}} > \dfrac{9}{8}\).
Vậy \(y > x\) hay \(x < y\)

Tìm \(x\) biết: \(x - 4,5 = 7,98\)
A. \(x = 52,98\)
B. \(x = 84,3\)
C. \(x = 8,43\)
D. \(x = 12,48\)
D. \(x = 12,48\)
\(x\) ở vị trí là số bị trừ, muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.
Ta có:
\(\begin{array}{l}x - 4,5 = 7,98\\x = 7,98 + 4,5\\x = 12,48\end{array}\)
Vậy \(x = 12,48\).

Cho \(4da{m^2} = \) $...$ \(d{m^2}\) .
Số thích hợp điền vào chỗ trống là:
A.\(40\)
B. \(400\)
C. \(4000\)
D. \(40000\)
D. \(40000\)
Áp dụng nhận xét, trong bảng đơn vị đo diện tích, hai đơn vị liền nhau hơn (kém) nhau \(100\) lần.
Ta có: \(1da{m^2} = 100{m^2} = 10000d{m^2}\) nên \(4da{m^2} = 40000d{m^2}\).

$316 - 15,74 \times \;8 $ $ ...$ $18,45 \times 7 + 60,93$
Dấu thích hợp điền vào chỗ chấm là:
A. \( = \)
B. \( > \)
C. \( < \)
A. \( = \)
- Tính kết quả của từng vế sau đó so sánh các kết quả đó với nhau
-Biểu thức có chứa phép cộng, trừ, nhân, chia thì ta tính phép nhân, chia trước; phép cộng, trừ sau.
Ta có:
$+) \;316 - 15,74 \times \;8 $$= 316 - 125,92 $ $= 190,08$
$+) \;18,45 \times 7 + 60,93 $$= 129,15 + 60,93 $ $= 190,08$
Mà $190,08 = 190,08$.
Vậy $316 - 15,74 \times \;8 $ $= 18,45 \times 7 + 60,93$