Trường hợp đồng dạng thứ hai (c.g.c)
Trường hợp đồng dạng thứ hai là gì?
1. Lý thuyết
Định lí Trường hợp đồng dạng thứ hai (cạnh – góc – cạnh):
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
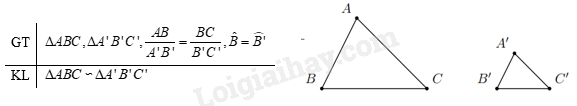
2. Ví dụ minh họa
Ví dụ 1: Cho hình thang ${ABCD}$ (${AB \parallel CD}$). Biết ${AB = 9}$ cm, ${BD = 12}$ cm và ${DC = 16}$ cm. Chứng minh $\Delta ABD\backsim \Delta BDC$.
Lời giải.
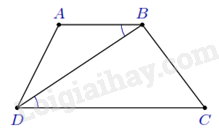
Ta có ${\widehat{ABD}=\widehat{BDC}}$ và ${\frac{BA}{BD}=\frac{DB}{DC}=\frac{3}{4}}$.
\(\Rightarrow \Delta ABD\backsim \Delta BDC\) (c.g.c).
Ví dụ 2: Cho tam giác ${ABC}$ có ${AB = 4}$ cm, ${AC = 8}$ cm. Trên cạnh ${AC}$ lấy ${D}$ sao cho ${AD = 2}$ cm. Chứng minh
a) ${\widehat{ABD} = \widehat{ACB}}$; b) ${BC = 2 BD}$.
Lời giải.
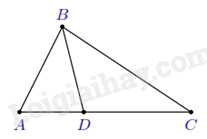
a) Xét $\Delta ABD$ và $\Delta ACB$ có
${\widehat{A}}$ chung, ${\frac{AD}{AB} = \frac{AB}{AC} = \frac{1}{2}}$
$\Rightarrow \Delta ABD\backsim \Delta ACB$ (c.g.c), suy ra ${\widehat{ABD} = \widehat{ACB}}$.
b) Từ câu a), ta có ${\frac{BC}{BD} = \frac{AC}{AB} = 2 \Rightarrow}$ đpcm.