Định lí Trường hợp đồng dạng thứ ba (góc – góc) — Không quảng cáo

1. Lý thuyết

Định lí Trường hợp đồng dạng thứ ba (góc – góc):

Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau (góc – góc).

2. Ví dụ minh họa

Ví dụ 1: Cho hình thang ${ABCD \: (AB \parallel CD)}$ có ${\widehat{DAB}=\widehat{DBC}}$. Chứng minh $\Delta ABD\backsim \Delta BDC$.

Lời giải

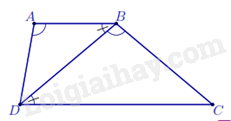
Ta có $\widehat{ABD}=\widehat{BDC}\Rightarrow \Delta ABD\backsim \Delta BDC$ (g.g).

Ví dụ 2: Cho tam giác ${ABC}$ cân tại $A\;(\hat{A}<{{90}^{0}})$, ${O}$ thuộc cạnh ${BC}$. Trên cạnh ${AB}$, ${AC}$ lần lượt lấy hai điểm ${M}$, ${N}$ sao cho ${\widehat{MON}=\widehat{ABC}}$. Chứng minh $\Delta BMO\backsim \Delta CON$.

Lời giải

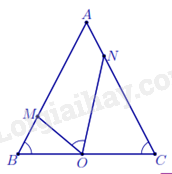
Ta có $\widehat{BMO}={{180}^{0}}-\widehat{ABC}-\widehat{MOB}$.

Mà $\widehat{MON}=\widehat{ABC}\Rightarrow \widehat{BMO}={{180}^{0}}-\widehat{MON}-\widehat{MOB}=\widehat{CON}$.

Chú ý $\widehat{MBO}=\widehat{OCN}\Rightarrow \Delta BMO\backsim \Delta CON$ (g.g).