Định nghĩa hai tam giác đồng dạng
Khi nào thì hai tam giác đồng dạng? Tam giác đồng dạng có tính chất gì?
1. Lý thuyết
- Định nghĩa tam giác đồng dạng:
Hai tam giác gọi là đồng dạng với nhau nếu chúng có ba cặp góc bằng nhau từng đôi một và ba cặp cạnh tương ứng tỉ lệ.
Chú ý:
Khi tam giác ABC đồng dạng với tam giác A’B’C’.
+ Ta viết $\Delta ABC\,\backsim \,\Delta A'B'C'$ với các đỉnh được ghi theo thứ tự các góc tương ứng bằng nhau.
+ Tỉ số các cạnh tương ứng $\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{CA}{C'A'}=k$ gọi là tỉ số đồng dạng.
- Tính chất của tam giác đồng dạng:
+ Mỗi tam giác đồng dạng với chính tam giác đó
+ Nếu $\Delta ABC\,\backsim \Delta A'B'C'$ thì $\Delta A'B'C'\backsim \,\Delta ABC$.
+ Nếu $\Delta A''B''C''\,\backsim \,\Delta A'B'C'$ và $\Delta A'B'C'\,\backsim \,\Delta ABC$ thì $\Delta A''B''C''\backsim \Delta ABC.$
2. Ví dụ minh họa
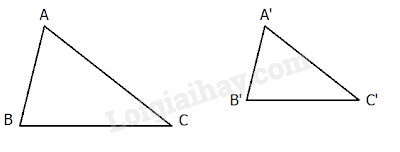
$\Delta ABC$ $\backsim $ $\Delta {A}'{B}'{C}'$$\Leftrightarrow \left\{ \begin{array}{*{35}{l}}\hat{A}=\hat{{A}'},\hat{B}=\hat{{B}'},\hat{C}=\hat{{C}'} \\ \frac{AB}{{A}'{B}'}=\frac{BC}{{B}'{C}'}=\frac{CA}{{C}'{A}'} \\ \end{array} \right.$