Giải bài 1.21 trang 18 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Từ đồ thị hàm số \(y = \cos {\rm{ }}x\), hãy vẽ các đồ thị hàm số sau:
Đề bài
Từ đồ thị hàm số \(y = \cos {\rm{ }}x\), hãy vẽ các đồ thị hàm số sau:
a) \(y = \, - \cos {\rm{ }}x\);
b) \(y = \,|\cos {\rm{ }}x|\);
c) \(y = \cos {\rm{ }}x + 1\);
d) \(y = \,\cos \left( {x + \frac{\pi }{2}} \right)\).
Phương pháp giải - Xem chi tiết
Từ đồ thị \(y = \cos {\rm{ }}x\), ta linh hoạt dịch chuyển đồ thị theo yêu cầu đề bài. Vẽ đồ thị \(y = \cos {\rm{ }}x\) bằng nét đứt và vẽ đồ thị trong đề bài bằng nét liền.
Lời giải chi tiết
a) Lấy đối xứng đồ thị hàm số \(y = \cos {\rm{ }}x\) qua trục hoành, ta được đồ thị hàm số \(y = \, - \cos {\rm{ }}x\).
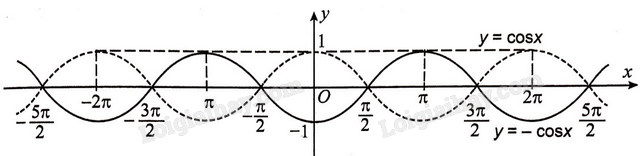
Trong hình trên, đồ thị hàm số \(y = \cos {\rm{ }}x\) là đường nét đứt còn đồ thị hàm số \(y = \, - \cos {\rm{ }}x\) là đường nét liền.
b) Ta có
\(y = \,|\cos {\rm{ }}x|\, = \left\{ \begin{array}{l}\cos x\,\,\,\,\,\,{\rm{khi}}\,\,\,\cos x \ge 0\\ - \cos x\,\,{\rm{khi}}\,\,\,\cos x < 0\end{array} \right.\)
Từ đó, để vẽ đồ thị hàm số \(y = \,|\cos {\rm{ }}x|\) ta vẽ đồ thị hàm số \(y = \cos {\rm{ }}x\) ở phía trên trục Ox và lấy đối xứng qua trục Ox phần đồ thị hàm số \(y = \cos {\rm{ }}x\) ở phía dưới trục Ox. Trong hình trên, đồ thị hàm số \(y = \cos {\rm{ }}x\) là đường nét đứt còn đồ thị hàm số \(y = \,|\cos {\rm{ }}x|\) là đường nét liền.

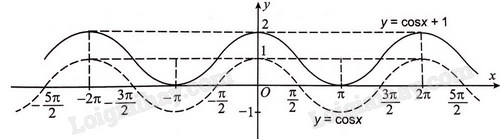
c) Để vẽ hàm số \(y = \cos {\rm{ }}x + 1\) đầu tiên ta vẽ hàm số \(y = \cos {\rm{ }}x\), sau đó dịch chuyển đồ thị này dọc theo trục Oy lên phía trên 1 đơn vị, ta được đồ thị hàm số. Trong hình dưới đây, đồ thị hàm số \(y = \cos {\rm{ }}x + 1\) là đường nét liền.
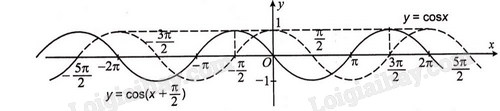
d) Để vẽ hàm số \(y = \,\cos \left( {x + \frac{\pi }{2}} \right)\) đầu tiên ta vẽ hàm số \(y = \cos {\rm{ }}x\), sau đó dịch chuyển đồ thị này dọc theo trục Ox sang bên trái \(\frac{\pi }{2}\) đơn vị, ta được đồ thị hàm số. Trong hình dưới đây, đồ thị hàm số \(y = \,\cos \left( {x + \frac{\pi }{2}} \right)\) là đường nét liền.