Giải bài 1 trang 63 vở thực hành Toán 8
Cho tam giác ABC; M và N lần lượt là trung điểm của hai cạnh AB và AC. Lấy điểm P sao cho N là trung điểm của đoạn thẳng MP.
Đề bài
Cho tam giác ABC; M và N lần lượt là trung điểm của hai cạnh AB và AC. Lấy điểm P sao cho N là trung điểm của đoạn thẳng MP.
a) Hỏi tứ giác AMCP là hình gì? Vì sao?
b) Với điều kiện nào của tam giác ABC thì tứ giác AMCP là hình chữ nhật; hình thoi; hình vuông?
Phương pháp giải - Xem chi tiết
a) Sử dụng dấu hiệu nhận biết hình bình hành.
b) Sử dụng hình chữ nhật; hình thoi; hình vuông.
Lời giải chi tiết
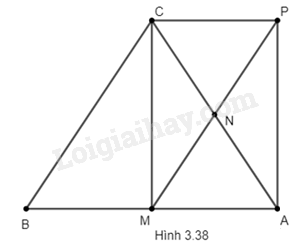
(H.3.38). a) Tứ giác AMCP có NC = NA, NM = NP nên AMCP là hình bình hành vì hai đường chéo cắt nhau tại trung điểm mỗi đường.
b) Hình bình hành AMCP là hình chữ nhật khi góc AMC là góc vuông. Góc AMC là góc vuông khi trung tuyến CM cũng là đường cao của tam giác ABC, tức là tam giác ABC cân tại C.
+) Hình bình hành AMCP là hình thoi khi và chỉ khi có hai cạnh kề bằng nhau AM = CM, tức là MC = MA = MC; khi đó tam giác CBA vuông tại C.
+) Từ hai phần trên, suy ra tứ giác AMCP là hình vuông khi và chỉ khi tam giác ABC vuông cân tại C.