Giải bài 1 trang 97 SGK Toán 10 tập 1 – Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:

a) $\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD}  = 4\overrightarrow {MO}$

b) $\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = 2\overrightarrow {AC}$

Lời giải chi tiết

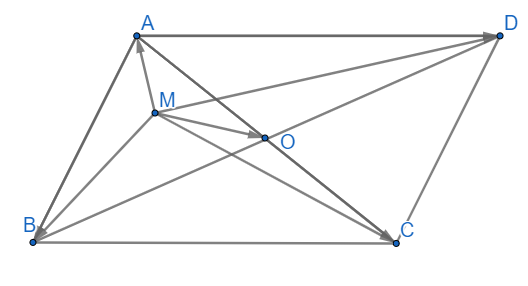
a) $\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD}  = 4\overrightarrow {MO}$

$\Leftrightarrow \overrightarrow {MO}  + \overrightarrow {OA}  + \overrightarrow {MO}  + \overrightarrow {OB}  + \overrightarrow {MO}  + \overrightarrow {OC}  + \overrightarrow {MO}  + \overrightarrow {OD}  = 4\overrightarrow {MO}$

$\Leftrightarrow 4\overrightarrow {MO}  + \left( {\overrightarrow {OA}  + \overrightarrow {OB} } \right) + \left( {\overrightarrow {OC}  + \overrightarrow {OD} } \right) = 4\overrightarrow {MO}$

$\Leftrightarrow 4\overrightarrow {MO}  + \overrightarrow 0  + \overrightarrow 0  = 4\overrightarrow {MO} \\ \Leftrightarrow 4\overrightarrow {MO}  = 4\overrightarrow {MO}$ (luôn đúng)

(vì O là giao điểm 2 đường chéo nên là trung điểm của AB, CD)

b) ABCD là hình bình hành nên ta có $\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC}$

Suy ra $\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} = \left( {\overrightarrow {AB}  + \overrightarrow {AD} } \right) + \overrightarrow {AC}  = \overrightarrow {AC}  + \overrightarrow {AC}  = 2\overrightarrow {AC}$ (đpcm)