Giải bài 10 trang 89 SGK Toán 8 tập 1– Chân trời sáng tạo
Cho tam giác
Đề bài
Cho tam giác \(ABC\) vuông tại \(A\) ( \(AB < AC\) ). Gọi \(M\) , \(N\) , \(E\) lần lượt là trung điểm của \(AB\) , \(AC\) , \(BC\)
a) Chứng minh rằng tứ giác \(ANEB\) là hình thang vuông
b) Chứng minh rằng tứ giác \(ANEM\) là hình chữ nhật
c) Qua \(M\) kẻ đường thẳng song song với \(BN\) cắt \(EN\) tại \(F\) . Chứng minh rằng tứ giác \(AFCE\) là hình thoi
d) Gọi \(D\) là điểm đối cứng của \(E\) qua \(M\) . Chứng minh rằng \(A\) là trung điểm của \(DF\)
Phương pháp giải - Xem chi tiết
a) Áp dụng dấu hiệu nhận biết hình thang vuông
b) Áp dụng dấu hiệu nhận biết hình chữ nhật
c) Áp dụng dấu hiệu nhận biết hình thoi
d) Chứng minh 3 điểm \(A\) , \(E\) , \(F\) thẳng hàng và \(AD = AF\) (do cùng bằng \(BE\) )
Lời giải chi tiết
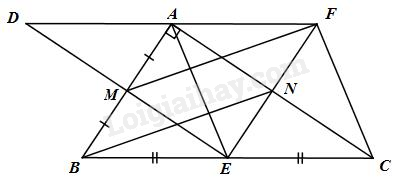
a) Xét tam giác ABC vuông tại A có E là trung điểm của BC nên AE là đường trung tuyến ứng với cạnh huyền của tam giác ABC nên AE = BE = EC = \(\frac{1}{2}\) BC.
Vì AE = EC nên E thuộc đường trung trực của AC. Vì N là trung điểm của AC nên N thuộc đường trung trực của AC.
=> EN là đường trung trực của AC hay \( EN \bot AC\)
Ta có \(AB \bot AC, EN \bot AC \Rightarrow AB // EN\) nên ANEB là hình thang.
Vì \(\widehat {BAN} = 90^0\) nên ANEB là hình thang vuông.
b) \(M\) , \(E\) lần lượt là trung điểm của \(AB\) và \(BC\) (gt);
Suy ra \(ME\) là đường trung bình của \(\Delta ABC\)
Suy ra \(ME\) // \(AC\) hay \(ME\) // \(AN\)
Mà \(AM\) // \(NE\) (do \(AB\) // \(NE\) )
Suy ra tứ giác \(AMEN\) là hình bình hành
Mà \(\widehat {{\rm{MAN}}} = 90^\circ \) nên \(AMEN\) là hình chữ nhật
c) Xét tứ giác \(BMFN\) có: \(MF\) // \(BN\) (gt) và \(BM\) // \(FN\) (do \(AB\) // \(NE\) )
Suy ra \(BMFN\) là hình bình hành
Suy ra \(BM = FN\)
Mặt khác \(NE = AM\) (Tứ giác \(ANEM\) là hình chữ nhật) và \(AM = BM\)
Suy ra \(FN = NE\)
Tứ giác \(AFCE\) có \(N\) là trung điểm của \(AC\) và \(EF\)
Suy ra \(AFCE\) là hình bình hành
Mà \(AC \bot EF\)
Do đó \(AFCE\) là hình thoi
d) Xét tứ giác \(ADBE\) ta có: \(DE\) và \(AB\) cắt nhau tại \(M\) (gt)
Mà \(M\) là trung điểm của \(AB\) (gt)
\(M\) là trung điểm của \(DE\) (do \(D\) đối xứng với \(E\) qua \(M\) )
Suy ra \(ADBE\) là hình bình hành
Suy ra \(AD\) // \(BE\) hay \(AD\) // \(EC\)
Mà \(AF\) // \(EC\) (do \(AECF\) là hình thoi)
Suy ra \(A,D,F\) thẳng hàng (1)
Mà \(ADBE\) là hình bình hành
Suy ra \(BE\) // \(AD\)
Mà \(AF = EC\) (do \(AFCE\) là hình thoi); \(EB = EC\) (gt)
Suy ra \(AD = AF\) (2)
Từ (1) và (2) suy ra \(A\) là trung điểm của \(DF\)