Giải Bài 11 trang 92 sách bài tập toán 7 tập 1 - Cánh diều
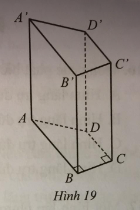
Cho hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ có đáy là hình thang ABCD vuông tại B (AB song song với CD) với
Đề bài
Cho hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ có đáy là hình thang ABCD vuông tại B ( AB song song với CD ) với \(AB = 9{\rm{ dm}}\), \(DC = 6{\rm{ dm}}\), \(BC = 4{\rm{ dm}}\), \(AD = 5{\rm{ dm}}\) và chiều cao \(AA' = 100{\rm{ cm}}\) (Hình 19).
a) Tính diện tích xung quanh của hình lăng trụ ABCD.A’B’C’D’ .
b) Tính thể tích của hình lăng trụ ABCD.A’B’C’D’ .
c) Người ta dán giấy màu (bên ngoài) tất cả các mặt của hình lăng trụ. Tính số tiền người đó phải trả, biết rằng giá tiền dán giấy màu mỗi mét vuông (bao gồm tiền công và nguyên vật liệu) là 150 000 đồng.
Phương pháp giải - Xem chi tiết
a) Công thức tính diện tích xung quanh của hình lăng trụ đứng tứ giác là: \({S_{xq}} = C{\rm{ }}.{\rm{ }}h\) ( C là chu vi đáy, h là chiều cao hình lăng trụ).
b) Công thức tính thể tích của hình lăng trụ đứng tứ giác là: \(V = S{\rm{ }}.{\rm{ }}h\) ( S là diện tích đáy, h là chiều cao hình lăng trụ).
c) Muốn tính số tiền người đó phải trả ta cần tính diện tích mà người đó dán giấy màu (bằng tổng diện tích các mặt).
Lời giải chi tiết
a) Đổi 100 cm = 10 dm.
Diện tích xung quang của hình lăng trụ ABCD.A’B’C’D’ là:
\(\left( {9 + 6 + 4 + 5} \right).10 = 240{\rm{ (d}}{{\rm{m}}^2})\).
b) Diện tích đáy ABCD của hình lăng trụ là:
\(\dfrac{{(9 + 6){\rm{ }}.{\rm{ }}4}}{2} = 30{\rm{ (d}}{{\rm{m}}^2})\).
Thể tích của hình lăng trụ ABCD.A’B’C’D’ là:
\(30{\rm{ }}{\rm{. 10 = 300 (d}}{{\rm{m}}^3})\).
c) Tổng diện tích tất cả các mặt của hình lăng trụ là:
\(240 + 30{\rm{ }}{\rm{. 2 = 300 (d}}{{\rm{m}}^2}) = 3{\rm{ (}}{{\rm{m}}^2})\).
Số tiền người đó phải trả là:
\(3{\rm{ }}{\rm{. 150 000 = 450 000}}\) (đồng).