Giải Bài 12 trang 70 sách bài tập toán 7 - Cánh diều — Không quảng cáo

Đề bài

Cho tam giác ABC có $\hat A = 3\hat B = 6\hat C$ .

a) Tìm số đo góc lớn nhất, góc bé nhất của tam giác ABC.

b) Kẻ AD vuông góc với BC tại D. Chứng minh AD < BD.

Lời giải chi tiết

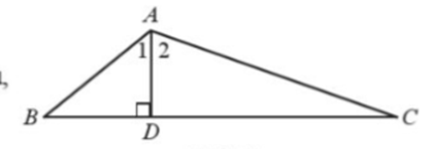
a) Từ $\hat A = 3\hat B = 6\hat C$ suy ra: $\frac{{\hat A}}{6} = \frac{{\hat B}}{2} = \frac{{\hat C}}{1}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{{\hat A}}{6} = \frac{{\hat B}}{2} = \frac{{\hat C}}{1} = \frac{{\hat A + \hat B + \hat C}}{{6 + 2 + 1}} = \frac{{180^\circ }}{9} = 20^\circ$

Suy ra

• $\hat A = 20^\circ .6 = 120^\circ ;$

• $\hat B = 20^\circ .2 = 40^\circ ;$

• $\hat C = 20^\circ .1 = 20^\circ .$

Vậy trong tam giác ABC, số đo góc lớn nhất là $\widehat {{A^{}}} = 120^\circ$, số đo góc bé nhất là $\hat C = 20^\circ$

b) Xét ∆ABD vuông tại D ta có:

${\hat A_1} + \hat B = 90^\circ$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Mà $\hat B = 40^\circ$ (câu a)

Suy ra ${\hat A_1} = 90^\circ  - \hat B = 90^\circ  - 40^\circ  = 50^\circ$.

Trong ∆ADB có: ${\hat A_1} > \hat B$ (do 50° > 40°).

Suy ra BD > AD (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn).

Vậy AD < BD.