Giải Bài 12 trang 107 sách bài tập toán 7 tập 1 - Cánh diều — Không quảng cáo

Đề bài

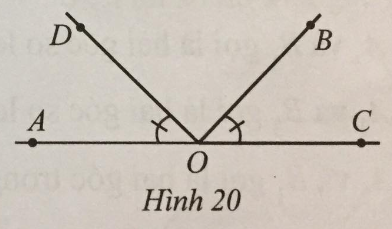
Ở Hình 20 có hai góc AOB và BOC là hai góc kề bù, $\widehat {AOB} = 3\widehat {BOC}$, $\widehat {AOD} = \widehat {BOC}$.

a) Tính số đo góc BOC .

b) Tia OB có là tia phân giác của góc COD hay không?

Lời giải chi tiết

a) Ta có:

$\begin{array}{l}\widehat {AOB} + \widehat {BOC} = \widehat {AOC} = 180^\circ  \to 3\widehat {BOC} + \widehat {BOC} = 180^\circ \\ \to 4\widehat {BOC} = 180^\circ  \Rightarrow \widehat {BOC} = \widehat {AOD} = 180^\circ :4 = 45^\circ \end{array}$

Vậy $\widehat {BOC} = 45^\circ$.

b) Ta có: $\widehat {BOD} = \widehat {AOC} - \widehat {AOD} - \widehat {BOC} = 180^\circ  - 45^\circ  - 45^\circ  = 90^\circ$.

Mà $\widehat {BOC} = 45^\circ  < \widehat {BOD} = 90^\circ$ nên tia OB không là tia phân giác của góc COD.