Giải bài 12 trang 59 SGK Toán 8 tập 2– Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho tam giác $ABC$ có $BC$ bằng 30cm. Trên đường cao $AH$ lấy các điểm $K,I$ sao cho $AK = KI = IH$. Qua $I$ và $K$ vẽ các đường $EF//BC,MN//BC\left( {E,M \in AB;F,N \in AC} \right)$.

a) Tính độ dài các đoạn thẳng $MN$ và $EF$.

b) Tính diện tích tứ giác $MNFE$ biết rằng diện tích tam giác $ABC$ là $10,8d{m^2}$.

Lời giải chi tiết

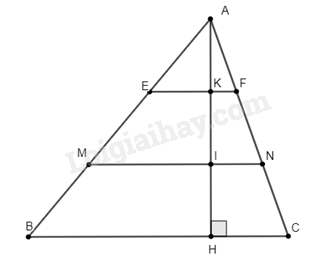
a) Vì $AK = KI = IH \Rightarrow AK = \frac{1}{3}AH;AI = \frac{2}{3}AH$.

Vì $EF//BC \Rightarrow EK//BH;MN//BC \Rightarrow MI//BH$

Xét tam giác $ABH$ ta có $EK//BH$, theo định lí Thales ta có:

$\frac{{AE}}{{AB}} = \frac{{AK}}{{AH}} = \frac{1}{3}$

Xét tam giác $ABH$ ta có $MI//BH$, theo định lí Thales ta có:

$\frac{{AM}}{{AB}} = \frac{{AI}}{{AH}} = \frac{2}{3}$

Xét tam giác $ABC$ ta có $EF//BC$, theo hệ quả của định lí Thales ta có:

$\frac{{AE}}{{AB}} = \frac{{EF}}{{BC}} = \frac{1}{3} \Rightarrow \frac{{EF}}{{30}} = \frac{1}{3} \Rightarrow EF = \frac{{30.1}}{3} = 10$

Xét tam giác $ABC$ ta có $MN//BC$, theo hệ quả của định lí Thales ta có:

$\frac{{AM}}{{AB}} = \frac{{MN}}{{BC}} = \frac{2}{3} \Rightarrow \frac{{MN}}{{30}} = \frac{2}{3} \Rightarrow MN = \frac{{30.2}}{3} = 20$

Vậy $EF = 10cm;MN = 20cm$.

b) Đổi $10,8d{m^2} = 1080c{m^2}$

Diện tích tam giác $ABC$ là:

${S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}AH.30 = 1080\left( {c{m^2}} \right)$

$\Rightarrow AH = 1080.2:30 = 72cm$

Ta có: $AH \bot BC \Rightarrow AH \bot MN$ (quan hệ từ vuông góc đến song song)

Do đó, $KI \bot MN$

Mà $KI = \frac{1}{3}AH \Rightarrow KI = \frac{1}{3}.72 = 24cm$

Tứ giác $MNFE$ có $MN//EF$ (cùng song song với $BC$) nên tứ giác $MNFE$ là hình thang.

Lại có: $KI \bot MN \Rightarrow KI$là đường cao của hình thang.

Diện tích hình thang $MNFE$ là:

${S_{MNFE}} = \frac{1}{2}\left( {EF + MN} \right).KI = \frac{1}{2}.\left( {10 + 20} \right).24 = 360\left( {c{m^2}} \right)$

Vậy diện tích tứ giác $MNFE$ là $360c{m^2}$.