Giải bài 12 trang 92 sách bài tập toán 8 - Cánh diều
Cho hình thang cân \(ABCD\) có \(AB//CD,AB < CD\), hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(P\), hai cạnh bên \(AD\) và \(BC\) kéo dài cắt nhau tại \(Q\).
Đề bài
Cho hình thang cân \(ABCD\) có \(AB//CD,AB < CD\), hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(P\), hai cạnh bên \(AD\) và \(BC\) kéo dài cắt nhau tại \(Q\). Chứng minh \(PQ\) là đường trung trực của hai đáy hình thang cân \(ABCD\).
Phương pháp giải - Xem chi tiết
Dựa vào tính chất của hình thang cân:
- Hai cạnh bên bằng nhau
- Hai đường chéo bằng nhau
Và sử dụng định nghĩa của đường trung trực: đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng gọi là đường trung trực của đoạn thẳng ấy.
Lời giải chi tiết
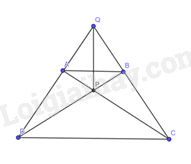
\(\Delta ACD = \Delta BDC\) (c.g.c). Suy ra \(\widehat {PCD} = \widehat {PDC}\)
Do đó, tam giác \(PCD\) cân tại \(P\). Suy ra \(PC = PD\)
Mà \(AC = BD\), suy ra \(PA = PB\)
Do \(AB//CD\) nên \(\widehat {QAB} = \widehat {ADC};\widehat {QBA} = \widehat {BCD}\) (các cặp góc đồng vị)
Mặt khác, \(\widehat {ADC} = \widehat {BCD}\) nên \(\widehat {QAB} = \widehat {QBA}\)
Do đó, tam giác \(QAB\) cân tại \(Q\). Suy ra \(QA = QB\)
Mà \(AD = BC\), suy ra \(QD = QC\)
Ta có: \(PA = PB,PC = PD\) và \(QA = QB,QC = QD\) nên \(PQ\) là đường trung trực của cả hai đoạn thẳng \(AB\) và \(CD\).