Giải bài 12 trang 94 sách bài tập toán 11 - Cánh diều — Không quảng cáo

Đề bài

Cho hình chóp S.ABC có $\widehat {ASB} = \widehat {BSC} = \widehat {CSA} = {90^0}.$Gọi H là trực tâm của tam giác ABC. Chứng minh rằng $SH \bot \left( {ABC} \right).$

Lời giải chi tiết

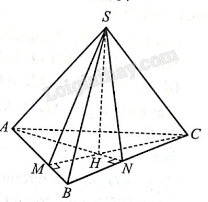
Gọi AN, CM là hai đường cao của tam giác ABC.

Gọi H là giao điểm của AN và CM.

Theo giả thiết, $SA \bot SB,{\rm{ }}SA \bot SC$ mà $SB \cap SC = S$ nên $SA \bot \left( {SBC} \right)$ mà $BC \subset \left( {SBC} \right) \Rightarrow SA \bot BC.$

Ngoài ra, $AH \bot BC$ và SA, AH cắt nhau trong mặt phẳng (SAH) nên $BC \bot \left( {SAH} \right) \Rightarrow BC \bot SH.$

Tương tự, ta có: $AB \bot SH.$

Bên cạnh đó, AB, BC cắt nhau trong mặt phẳng (ABC) nên $SH \bot \left( {ABC} \right).$