Giải bài 13 trang 74 sách bài tập toán 8 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Tính chiều cao của hình thang cân ABCD biết rằng cạnh bên $BC = 25cm$ và các cạnh đáy $AB = 10cm,CD = 24cm$.

Lời giải chi tiết

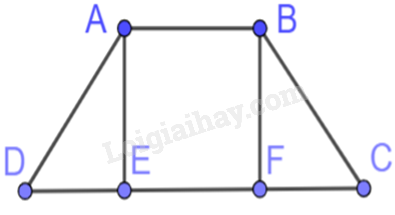
Kẻ $AE \bot DC,BF \bot DC\left( {E,F \in DC} \right)$ nên $\widehat {AED} = \widehat {AEF} = \widehat {BFE} = \widehat {BFC} = {90^0}$

Vì ABCD là hình thang cân nên $\widehat D = \widehat C$, $AD = BC$

Tam giác AED và tam giác BFC có:

$\widehat {AED} = \widehat {BFC} = {90^0}$, $\widehat D = \widehat C$, $AD = BC$

Do đó, $\Delta AED = \Delta BFC\left( {ch - gn} \right)$. Suy ra $DE = CF$

Tứ giác ABFE có: AB//EF, AE//BF (cùng vuông góc với DC) nên tứ giác ABFE là hình bình hành. Do đó, $AB = FE = 10cm$

Suy ra: $DE = FC = \frac{{DC - EF}}{2} = \frac{{24 - 10}}{2} = 7\left( {cm} \right)$

Áp dụng định lí Pythagore vào tam giác ADE vuông tại E có: $A{E^2} = A{D^2} - D{E^2} = {25^2} - {7^2} = 576$, suy ra $AE = 24cm$