Giải bài 17 trang 80 SBT toán 10 - Cánh diều
Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C.
Đề bài
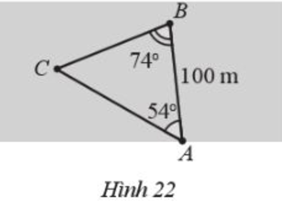
Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C . Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng AB = 100 m. Hai người tiến hành đo đạc và thu được kết quả: \(\widehat {CAB} = {54^0},\widehat {CBA} = {74^0}\) (Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đến hàng phần mười theo đơn vị mét)?
Phương pháp giải - Xem chi tiết
Bước 1: Tính số đo góc \(\widehat {ACB}\)
Bước 2: Sử dụng định lí sin để tính độ dài BC của ∆ ABC rồi kết luận
Lời giải chi tiết
Ta có: \(\widehat {ACB} = {180^0} - (\widehat {CBA} + \widehat {CAB}) = {52^0}\)
Áp dụng định lí sin cho ∆ ABC ta có: \(\frac{{BC}}{{\sin \widehat {CAB}}} = \frac{{AB}}{{\sin \widehat {ACB}}} \Rightarrow BC = \frac{{AB.\sin \widehat {CAB}}}{{\sin \widehat {ACB}}} = \frac{{100.\sin {{54}^0}}}{{\sin {{52}^0}}} \approx 102,7\)
Vậy con tàu cách hòn đảo 102,7 m