Giải bài 2 trang 27 sách bài tập toán 10 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ Oxy

a) \(x + y - 1 > 0\)

b) \(x - 1 \ge 0\)

c) \( - y + 2 \le 0\)

Lời giải chi tiết

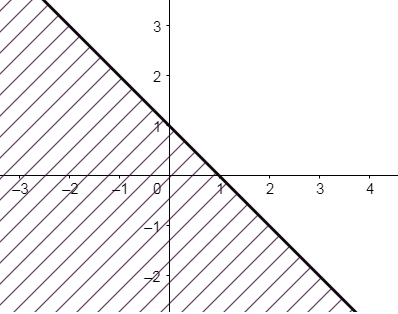
a) Vẽ đường thẳng \({d_1}:x + y - 1 = 0\) đi qua hai điểm \(A\left( {0;1} \right)\) và \(B\left( {1;0} \right)\)

Xét gốc tọa độ \(O\left( {0;0} \right)\)

Ta thấy \(O \notin {d_1}\) và \(2.0 - 5.0 + 10 = 10 > 0\). Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \({d_1}\) và không chứa gốc tọa độ O (miền không gạch chéo như hình dưới)

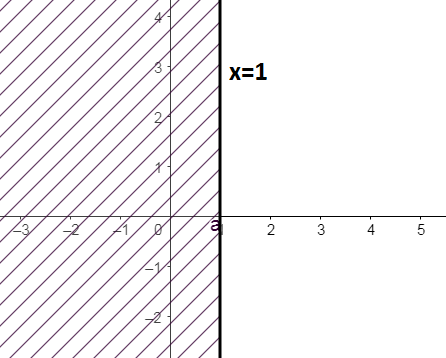
b) Vẽ đường thẳng \({d_2}:x - 1 = 0\)song song với trục tung và đi qua điểm \(A\left( {1;0} \right)\)

Xét gốc tọa độ \(O\left( {0;0} \right)\)

Ta thấy \(O \notin {d_2}\) và \(0 - 1 =  - 1 < 0\). Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa bờ \({d_2}\) và không chứa gốc tọa độ O (miền không gạch chéo như hình dưới)

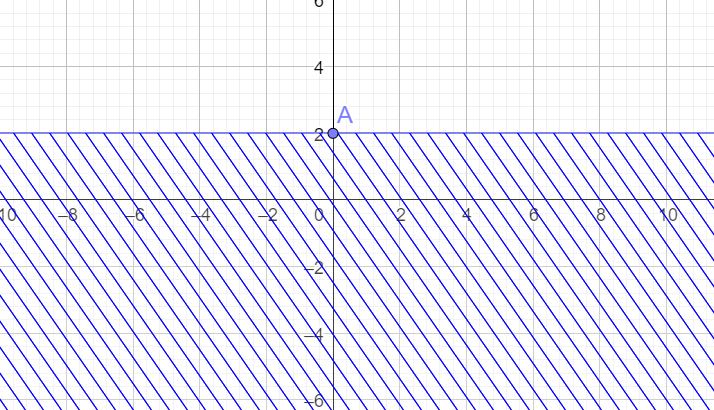
c) Vẽ đường thẳng \({d_3}: - y + 2 = 0\)song song với trục hoành và đi qua điểm \(A\left( {0;2} \right)\)

Xét gốc tọa độ \(O\left( {0;0} \right)\)

Ta thấy \(O \notin {d_3}\) và \( - 0 + 2 = 2 > 0\). Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa bờ \({d_3}\) và không chứa gốc tọa độ O (miền không gạch chéo như hình dưới)