Giải bài 2 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Cho ∆ABC đều có cạnh bằng 2. Qua ba phép biến hình liên tiếp: Phép tịnh tiến, phép quay \({Q_{\left( {B,{\rm{ }}60^\circ } \right)}},\)
Đề bài
Cho ∆ABC đều có cạnh bằng 2. Qua ba phép biến hình liên tiếp: Phép tịnh tiến, phép quay \({Q_{\left( {B,{\rm{ }}60^\circ } \right)}},\) phép vị tự \({V_{\left( {A,{\rm{ }}3} \right)}},\)∆ABC biến thành \(\Delta {A_1}{B_1}{C_1}.\) Tìm diện tích \(\Delta {A_1}{B_1}{C_1}.\)
Phương pháp giải - Xem chi tiết
\({S_{\Delta ABC}} = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}BC.BA.\sin B = \frac{1}{2}CA.CB.\sin C\)
Lời giải chi tiết
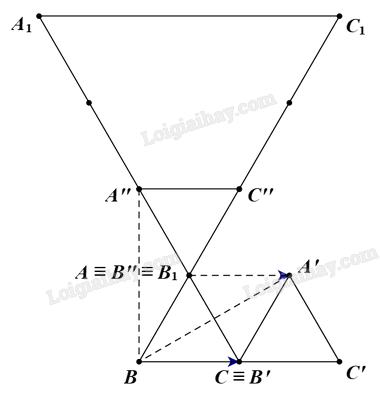
Ta có \(\Delta \)ABC đều có cạnh bằng 2. Suy ra \(AB{\rm{ }} = {\rm{ }}AC{\rm{ }} = {\rm{ }}2\) và \(\widehat {BAC} = {60^o}\).
Vì phép tịnh tiến và phép quay đều là phép dời hình nên ảnh của \(\Delta \)ABC qua phép tịnh tiến \({T_{\overrightarrow {BC} }}\) và phép quay \({Q_{\left( {B,{\rm{ }}60^\circ } \right)}}\;\) đều có các kích thước bằng các kích thước tương ứng của \(\Delta \)ABC.
Gọi f là phép biến hình có được bằng thực hiện hai phép biến hình liên tiếp là phép tịnh tiến và phép quay \({Q_{\left( {B,{\rm{ }}60^\circ } \right)}}.\)
Suy ra f là phép dời hình.
Do đó phép đồng dạng tỉ số 3 có được bằng cách thực hiện liên tiếp phép dời hình f và phép vị tự \({V_{(A,{\rm{ }}3)}}\) biến \(\Delta \)ABC thành \(\Delta {A_1}{B_1}{C_1}\).
Vì vậy phép đồng dạng tỉ số 3 biến các điểm A, B, C theo thứ tự thành các điểm \({A_1},{\rm{ }}{B_1},{\rm{ }}{C_1}.\)
Khi đó \({A_1}{B_1}\; = {\rm{ }}3AB{\rm{ }} = {\rm{ }}3.2{\rm{ }} = {\rm{ }}6\) và \({A_1}{C_1}\; = {\rm{ }}3AC{\rm{ }} = {\rm{ }}3.2{\rm{ }} = {\rm{ }}6.\)
Vì \(\Delta \)ABC và \(\Delta \)A 1 B 1 C 1 đồng dạng với nhau nên \(\widehat {{B_1}{A_1}{C_1}} = \widehat {BAC} = {60^o}\)
Ta có \({S_{\Delta {A_1}{B_1}{C_1}}} = \frac{1}{2}{A_1}{B_1}.{A_1}{C_1}.\sin \widehat {{B_1}{A_1}{C_1}} = \frac{1}{2}.6.6.\sin {60^o} = 9\sqrt 3 \)
Vậy diện tích \(\Delta {A_1}{B_1}{C_1}\) bằng \(9\sqrt 3 \).