Giải Bài 2 trang 60 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác của góc A. Chứng minh tam giác ABC là tam giác cân.
Đề bài
Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác của góc A. Chứng minh tam giác ABC là tam giác cân.
Phương pháp giải - Xem chi tiết
- Chứng minh: \(\Delta AMH = \Delta AMK\)suy ra: MH = MK
- Chứng minh: \(\widehat B = \widehat C\) suy ra tam giác ABC cân
Lời giải chi tiết
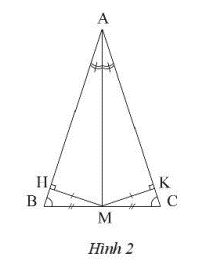
Vẽ đường cao MH của tam giác AMB và vẽ đường cao MK của tam giác AMC.
Ta có \(\Delta AMH = \Delta AMK\)(vì hai tam giác vuông có chung cạnh huyền AM, và một góc nhọn bằng nhau)
Suy ra: MH = MK.
Từ đó, ta có: \(\Delta MBH = \Delta MCK\) (hai tam giác vuông có chung cạnh huyền Am và một cạnh góc vuông bằng nhau: MH = MK)
Suy ra \(\widehat B = \widehat C\)
Vậy tam giác ABC là tam giác cân tại A.
Cùng chủ đề:
Giải Bài 2 trang 60 sách bài tập toán 7 - Chân trời sáng tạo