Giải Bài 2 trang 63 sách bài tập toán 7 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho tam giác ABC cân tại A, vẽ đường trung tuyến AM. Qua A vẽ đường thẳng d vuông góc với AM. Chứng minh d // BC.

Lời giải chi tiết

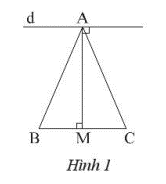
Ta có: \(\Delta AMB = \Delta AMC\) (c – c – c) vì cạnh AM chung, AB = AC (tam giác ABC cân tại A), MB = MC (AM là đường trung tuyến)

Suy ra: \(\widehat {AMB} = \widehat {AMC} = \frac{{{{180}^o}}}{2} = {90^o}\)

Ta có d và BC cùng vuông góc với AM suy ra d // BC.