Giải bài 2 trang 74 sách bài tập toán 8 - Chân trời sáng tạo tập 2
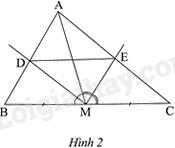
Cho Hình 2, biết AM là đường trung tuyến của tam giác ABC, MD là tia phân giác của \(\widehat {AMB}\), ME là tia phân giác của \(\widehat {AMC}\). Chứng minh rằng \(\Delta ADE\backsim \Delta ABC\).
Đề bài
Cho Hình 2, biết AM là đường trung tuyến của tam giác ABC, MD là tia phân giác của \(\widehat {AMB}\), ME là tia phân giác của \(\widehat {AMC}\). Chứng minh rằng \(\Delta ADE\backsim \Delta ABC\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về định lí về hai tam giác đồng dạng để chứng minh: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết
Tam giác AMB có MD là đường phân giác của \(\widehat {AMB}\) nên \(\frac{{DA}}{{DB}} = \frac{{MA}}{{MB}}\).
Tam giác AMC có ME là đường phân giác của \(\widehat {AMC}\) nên \(\frac{{EA}}{{EC}} = \frac{{MA}}{{MC}}\).
Mà \(MB = MC\) nên \(\frac{{DA}}{{DB}} = \frac{{EA}}{{EC}}\)
Tam giác ABC có: \(\frac{{DA}}{{DB}} = \frac{{EA}}{{EC}}\) nên DE//BC. Vậy \(\Delta ADE\backsim \Delta ABC\)