Giải bài 2 trang 80 SGK Toán 8 tập 1– Chân trời sáng tạo — Không quảng cáo

Đề bài

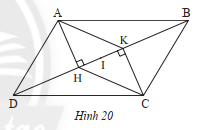
Cho hình bình hành \(ABCD\) , kẻ \(AH\) vuông góc với \(BD\) tại \(H\) và \(CK\) vuông góc với \(BD\) tại \(K\) (Hình 20)

a) Chứng minh tứ giác \(AHCK\) là hình bình hành

b) Gọi \(I\) là trung điểm của \(HK\) .Chứng minh \(IB = ID\)

Lời giải chi tiết

a) Vì \(AH\) , \(CK\) vuông góc với \(BD\) (gt)

Suy ra \(AH\) // \(CK\)

Vì \(ABCD\) là hình bình hành (gt)

Suy ra \(AD = BC\) ; \(AD\) // \(BC\)

Xét \(\Delta ADH\) và \(\Delta CBK\) ta có:

\(\widehat {{\rm{AHD}}} = \widehat {{\rm{CKB}}} = 90^\circ \) (gt)

\(AD = BC\) (cmt)

\(\widehat {{\rm{ADH}}} = \widehat {{\rm{CBK}}}\) (do \(AD\) // \(BC\) )

Suy ra \(\Delta ADH = \Delta CBK\) (ch-gn)

Suy ra \(AH = CK\) (hai cạnh tương ứng)

Mà \(AH\) // \(CK\) (cmt)

Suy ra \(AHCK\) là hình bình hành

b) Vì \(AHCK\) là hình bình hành nên hai đường chéo \(HK\) và \(AC\) cắt nhau tại trung điểm.

Mà \(I\) là trung điểm của \(HK\).

Suy ra \(I\) là trung điểm của \(AC\).

Ta lại có \(ABCD\) là hình bình hành nên hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm.

Suy ra \(I\) là trung điểm của \(BD\) hay \( IB = ID\)