Giải bài 2 trang 71 SGK Toán 8 – Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho tứ giác $ABCD$ có $AB = AD$ , $BD$ là tia phân giác của góc $B$ . Chứng minh rằng $ABCD$ là hình thang.

Lời giải chi tiết

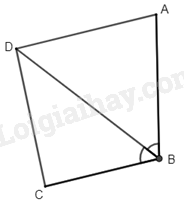
Xét $\Delta ABD$ ta có: $AD = AB$ (gt) nên $\Delta ADB$ cân tại $A$

Suy ra $\widehat {ADB} = \widehat {ABD}$

Mà $\widehat {ABD} = \widehat {CBD}$ (do $BD$ là phân giác của góc $B$ )

Do đó $\widehat {ADB} = \widehat {CBD}$

Mà hai góc ở vị trí so le trong

Suy ra $AD\;{\rm{//}}\;BC$

Suy ra $ABCD$ là hình thang