Giải Bài 26 trang 73 sách bài tập toán 7 - Cánh diều — Không quảng cáo

Đề bài

Cho ∆ABC = ∆MNP. Hai tia phân giác của góc B và C cắt nhau tại O tạo thành góc BOC bằng 120°. Tính tổng số đo các góc MNP và MPN của tam giác MNP.

Lời giải chi tiết

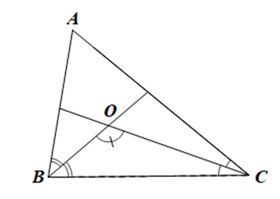
Vì BO là phân giác của góc ABC nên$\widehat {ABO} = \widehat {CBO} = \frac{{\widehat {ABC}}}{2}$

Vì CO là phân giác của góc ACB nên $\widehat {ACO} = \widehat {BCO} = \frac{{\widehat {ACB}}}{2}$

Xét DCOB ta có: $\widehat {BOC} + \widehat {OBC} + \widehat {OCB} = 180^\circ$ (tổng ba góc của một tam giác)

Suy ra $\widehat {OBC} + \widehat {OCB} = 180^\circ  - \widehat {BOC} = 180^\circ  - 120^\circ  = 60^\circ .$

Mà $\widehat {CBO} = \frac{{\widehat {ABC}}}{2},\widehat {BCO} = \frac{{\widehat {ACB}}}{2}.$

Suy ra $\frac{{\widehat {ABC}}}{2} + \frac{{\widehat {ACB}}}{2} = 60^\circ$

Do đó $\widehat {ABC} + \widehat {ACB} = 2.60^\circ  = 120^\circ .$

Mặt khác ∆ABC = ∆MNP nên ta có:

$\widehat {ABC} = \widehat {MNP}$ và $\widehat {ACB} = \widehat {MPN}$ (các cặp góc tương ứng).

Suy ra $\widehat {MNP} + \widehat {MPN} = \widehat {ABC} + \widehat {ACB} = 120^\circ$

Vậy $\widehat {MNP} + \widehat {MPN} = 120^\circ$