Giải bài 27 trang 99 sách bài tập toán 11 - Cánh diều — Không quảng cáo

Đề bài

Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), \(AB \bot BC\), \(SA = AB = 3a\), \(BC = 4a\). Gọi \(\alpha \), \(\beta \), \(\gamma \) lần lượt là số đo của các góc nhị diện \(\left[ {B,SA,C} \right]\), \(\left[ {A,BC,S} \right]\), \(\left[ {A,SC,B} \right]\). Tính

a) \(\cos \alpha \), \(\cos \beta \).

b*) \(\cos \gamma \).

Lời giải chi tiết

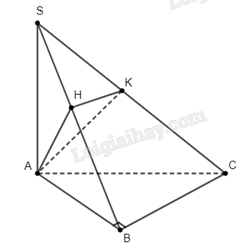
a) Do \(SA \bot \left( {ABC} \right)\) nên ta suy ra \(SA \bot AB\), \(SA \bot AC\) và \(SA \bot BC\). Suy ra \(\widehat {BAC}\) chính là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,C} \right]\), tức là \(\alpha  = \widehat {BAC}\).

Tam giác \(ABC\) vuông tại \(B\), nên \(AC = \sqrt {A{B^2} + A{C^2}}  = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}}  = 5a\).

Như vậy \(\cos \alpha  = \cos \widehat {BAC} = \frac{{AB}}{{AC}} = \frac{{3a}}{{5a}} = \frac{3}{5}\).

Tam giác \(ABC\) vuông tại \(B\), ta cũng suy ra \(BC \bot AB\). Do \(SA \bot BC\) nên ta suy ra \(BC \bot \left( {SAB} \right)\). Điều này dẫn tới \(BC \bot SB\).

Vì \(BC \bot SB\), \(BC \bot AB\) nên góc \(\widehat {SBA}\) chính là góc phẳng nhị diện của góc nhị diện \(\left[ {A,SC,B} \right]\), tức là \(\beta  = \widehat {SBA}\).

Tam giác \(SBA\) vuông tại \(A\), nên \(SB = \sqrt {S{A^2} + A{B^2}}  = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {3a} \right)}^2}}  = 3\sqrt 2 a\).

Như vậy \(\cos \beta  = \cos \widehat {SBA} = \frac{{AB}}{{SB}} = \frac{{3a}}{{3\sqrt 2 a}} = \frac{{\sqrt 2 }}{2}\).

b) Gọi \(H\) và \(K\) lần lượt là hình chiếu của \(A\) trên \(SB\) và \(SC\).

Theo câu a, ta có \(BC \bot \left( {SAB} \right)\) nên \(BC \bot AH\). Mà ta có \(AH \bot SB\) nên suy ra \(AH \bot \left( {BSC} \right)\), điều này dẫn tới \(AH \bot SC\).

Do \(AH \bot SC\), \(AK \bot SC\) nên \(SC \bot \left( {AHK} \right)\), suy ra \(HK \bot SC\).

Như vậy ta có \(AK \bot SC\), \(HK \bot SC\) nên \(\widehat {AKH}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,SC,H} \right]\). Do \(H \in \left( {SCB} \right)\) nên góc nhị diện \(\left[ {A,SC,H} \right]\) cũng chính là góc nhị diện \(\left[ {A,SC,B} \right]\). Do đó, \(\widehat {AKH}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,SC,B} \right]\), tức là \(\gamma  = \widehat {AKH}\).

Vì \(AH \bot \left( {BSC} \right)\) nên \(AH \bot HK\), do đó \(\cos \widehat {AKH} = \frac{{HK}}{{AK}}\).

Ta có \(AH = \frac{{SA.AB}}{{SB}} = \frac{{3a.3a}}{{3\sqrt 2 a}} = \frac{{3a\sqrt 2 }}{2}\) (do \(\Delta SAB\) vuông tại \(A\))

Và \(AK = \frac{{SA.AC}}{{SC}} = \frac{{3a.5a}}{{\sqrt {{{\left( {3a} \right)}^2} + {{\left( {5a} \right)}^2}} }} = \frac{{15{a^2}}}{{a\sqrt {34} }} = \frac{{15\sqrt {34} a}}{{34}}\) (do \(\Delta SAC\) vuông tại \(A\))

Suy ra \(HK = \sqrt {A{K^2} - A{H^2}}  = \sqrt {{{\left( {\frac{{15a\sqrt {34} }}{{34}}} \right)}^2} - {{\left( {\frac{{3a\sqrt 2 }}{2}} \right)}^2}}  = \frac{{6a\sqrt {17} }}{{17}}\).

Do đó, \(\cos \gamma  = \cos \widehat {AKH} = \frac{{HK}}{{AK}} = \frac{{\frac{{6a\sqrt {17} }}{{17}}}}{{\frac{{15a\sqrt {34} }}{{34}}}} = \frac{{2\sqrt 2 }}{5}\).