Giải bài 27 trang 99 sách bài tập toán 8 - Cánh diều
Cho một hình thoi có độ dài hai đường chéo là (frac{{18}}{5}) m và (frac{{27}}{{10}}) m. Tính chu vi và diện tích của hình thoi đó.
Đề bài
Cho một hình thoi có độ dài hai đường chéo là \(\frac{{18}}{5}\) m và \(\frac{{27}}{{10}}\) m. Tính chu vi và diện tích của hình thoi đó.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất của hình thoi:
Trong một hình thoi:
- Các cạnh đối song song
- Các góc đối bằng nhau
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
- Hai đường chéo là các đường phân giác của các góc ở đỉnh.
Và dựa vào định lí Pythagore: trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết
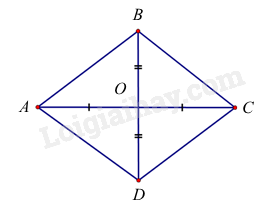
Xét hình thoi \(ABCD\) có \(AC = \frac{{18}}{5}m\), \(BD = \frac{{27}}{{10}}m\).
Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\).
Do \(ABCD\) là hình thoi nên \(AC \bot BD,O\) là trung điểm của \(AC\) và \(BD\).
Ta tính được:
\(OA = \frac{{AC}}{2} = \frac{9}{5}m\)
\(OB = \frac{{BD}}{2} = \frac{{27}}{{20}}m\).
Trong tam giác \(OAB\) vuông tại \(O\), ta có: \(A{B^2} = O{A^2} + O{B^2}\). Suy ra \(AB = \frac{9}{4}m\)
Chu vi của hình thoi \(ABCD\) là: \(4.\frac{9}{4} = 9\left( m \right)\)
Diện tích của hình thoi \(ABCD\) là: \(\frac{1}{2}.\frac{{18}}{5}.\frac{{27}}{{10}} = \frac{{243}}{{50}}\left( {{m^2}} \right)\).