Giải bài 28 trang 100 sách bài tập toán 11 - Cánh diều — Không quảng cáo

Đề bài

Cho hình chóp $S.ABCD$ có $ABCD$ là hình vuông, $AC$ cắt $BD$ tại $O$, $SO \bot \left( {ABCD} \right)$. Tất cả các cạnh của hình chóp bằng $a$.

a) Tính góc giữa đường thẳng $SB$ và mặt phẳng $\left( {SAC} \right)$.

b) Gọi $\alpha$ là số đo của góc nhị diện $\left[ {S,CD,A} \right]$. Tính $\cos \alpha$.

c) Gọi $d$ là giao tuyến của hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SCD} \right)$, $\beta$ là số đo của góc nhị diện $\left[ {A,d,D} \right]$. Tính $\cos \beta$.

d*) Gọi $\gamma$ là số đo góc nhị diện $\left[ {B,SC,D} \right]$. Tính $\cos \gamma$.

Lời giải chi tiết

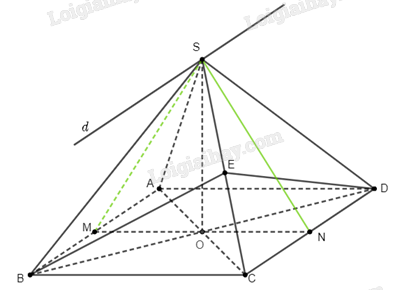
a) Do $SO \bot \left( {ABCD} \right)$, ta có $SO \bot OB$. Vì $ABCD$ là hình vuông nên $BO \bot AC$. Như vậy $BO \bot \left( {SAC} \right)$, tức là hình chiếu của điểm $B$ trên $\left( {SAC} \right)$. Do đó góc giữa $SB$ và $\left( {SAC} \right)$ là góc $\widehat {BSO}$.

Ta có $ABCD$ là hình vuông cạnh $a$, nên $BD = a\sqrt 2$.

Tam giác $SBD$ có $SB = SD = a$ và $S{B^2} + S{D^2} = {a^2} + {a^2} = 2{a^2} = B{D^2}$, nên tam giác này là tam giác vuông cân tại $S$.

Hơn nữa, do $SO \bot BD$, ta suy ra $\widehat {BSO} = \widehat {SBO} = {45^o}$.

Như vậy, góc giữa $SB$ và $\left( {SAC} \right)$ bằng ${45^o}$.

b) Gọi $N$ là trung điểm của $CD$. Do tam giác $SCD$ đều ($SC = SD = CD = a$), ta suy ra $SN \bot CD$ và $SN = \sqrt {S{C^2} - C{N^2}}  = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}}  = \frac{{a\sqrt 3 }}{2}$.

Do $O$ là tâm của hình vuông $ABCD$, ta suy ra $ON \bot CD$. Như vậy, góc phẳng nhị diện của góc nhị diện $\left[ {S,CD,O} \right]$ là góc $\widehat {SNO}$. Hơn nữa do $O \in \left( {ABCD} \right)$, ta suy ra góc nhị diện $\left[ {S,CD,O} \right]$ cũng chính là góc nhị diện $\left[ {S,CD,A} \right]$, tức là $\alpha  = \widehat {SNO}$.

Như vậy $\cos \alpha  = \cos \widehat {SNO} = \frac{{ON}}{{SN}} = \frac{{\frac{a}{2}}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt 3 }}{3}$.

c) Ta thấy rằng $AB\parallel CD$, $AB \subset \left( {SAB} \right)$, $CD \subset \left( {SCD} \right)$, $S \in \left( {SAB} \right) \cap \left( {SCD} \right)$, nên giao tuyến $d$ của hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SCD} \right)$ đi qua $S$ và song song với $AB$ và $CD$.

Gọi $M$ là trung điểm của $AB$. Tam giác $SAB$ đều ($SA = AB = SB = a$) nên $SM \bot AB$. Mặt khác, do $d\parallel AB$ nên $SM \bot d$. Chứng minh tương tự ta cũng có $SN \bot d$. Suy ra góc phẳng nhị diện của góc nhị diện $\left[ {M,d,N} \right]$ là góc $\widehat {MSN}$.

Hơn nữa, do $AM\parallel d$ và $DN\parallel d$, ta suy ra góc nhị diện $\left[ {M,d,N} \right]$ cũng chính là $\left[ {A,d,D} \right]$, tức là $\beta  = \widehat {MSN}$.

Ta có $SM = SN = \frac{{a\sqrt 3 }}{2}$, $MN = a$. Theo định lí cos trong tam giác, ta có:

$\cos \beta  = \cos \widehat {MSN} = \frac{{S{M^2} + S{N^2} - M{N^2}}}{{2SM.SN}} = \frac{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} - {a^2}}}{{2.\frac{{a\sqrt 3 }}{2}.\frac{{a\sqrt 3 }}{2}}} = \frac{1}{3}$.

d) Gọi $E$ là hình chiếu của $B$ trên $SC$. Theo câu a, ta có $BD \bot \left( {SAC} \right)$ nên suy ra $BD \bot SC$. Mà $BE \bot SC$ nên suy ra $SC \bot \left( {BDE} \right)$, điều này dẫn tới $SC \bot DE$.

Như vậy, vì $BE \bot SC$, $SC \bot DE$ nên góc phẳng nhị diện của góc nhị diện  $\left[ {B,SC,D} \right]$ là góc $\widehat {BED}$, tức là $\gamma  = \widehat {BED}$.

Tam giác $SBC$ đều ($SB = SC = BC = a$)  và có $BE \bot SC$, nên ta dễ dàng tính được $BE = \frac{{a\sqrt 3 }}{2}$. Tương tự, ta cũng có $DE = \frac{{a\sqrt 3 }}{2}$.

Theo định lí cos trong tam giác, ta có:

$\cos \gamma  = \cos \widehat {BED} = \frac{{B{E^2} + D{E^2} - B{D^2}}}{{2BE.DE}} = \frac{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {a\sqrt 2 } \right)}^2}}}{{2.\frac{{a\sqrt 3 }}{2}.\frac{{a\sqrt 3 }}{2}}} = \frac{{ - 1}}{3}$.