Giải bài 3.10 trang 56 SGK Toán 8 tập 1 - Kết nối tri thức
Cho hình thang cân ABCD (AB // CD) có AB = AD.
Đề bài
Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết \(\widehat {AB{\rm{D}}} = {30^o}\) , tính số đo các góc của hình thang đó.
Phương pháp giải - Xem chi tiết
Áp dụng định lí tổng các góc trong một tứ giác bằng \(360^0\)
Lời giải chi tiết
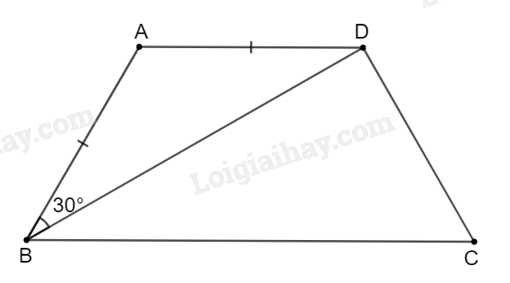
Xét tam giác ABD cân tại A (vì AB = AD), ta có:
• \(\widehat {AB{\rm{D}}} = \widehat {A{\rm{D}}B} = {30^o}\)
• \(\widehat A + \widehat {AB{\rm{D}}} + \widehat {A{\rm{D}}B} = {180^o}\) hay \(\widehat A + {30^o} + {30^o} = {180^o}\)
Suy ra \(\widehat A\)=180°−30°−30°=120 o
Vì AB // CD nên \(\widehat {A{\rm{B}}D} = \widehat {B{\rm{D}}C} = {30^o}\) (hai góc so le trong).
Do đó \(\widehat {ADC} = \widehat {A{\rm{D}}B} + \widehat {C{\rm{D}}B}\)=30°+30°=60°
Vì tứ giác ABCD là hình thang cân nên \(\widehat {ADC} = \widehat C\)=60°
Ta có: \(\widehat A + \widehat {ABC} + \widehat C + \widehat {A{\rm{D}}C} = {360^o}\)
120°+60°+60°+\(\widehat {A{\rm{B}}C}\)=360°
240°+\(\widehat {A{\rm{B}}C}\)=360°
Suy ra =360°−240°=120°
Vậy số đo các góc của hình thang ABCD là \(\widehat A = {120^o};\widehat {ABC} = {120^o};\widehat {C} = {60^o};\widehat {A{\rm{D}}C} = {60^o}\).