Giải bài 3.45 trang 75 SGK Toán 8 tập 1 - Kết nối tri thức
Cho tam giác ABC cân tại A
Đề bài
Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C. Gọi E và K lần lượt là chân đường vuông góc hạ từ M và từ B xuống AC, còn N, D lần lượt là chân đường vuông góc hạ từ B xuống ME và từ M xuống AB. (H.3.60)
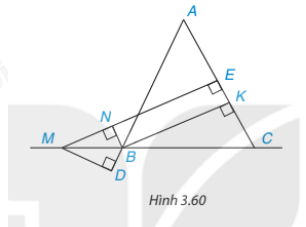
Chứng minh rằng:
a) Tứ giác BKEN là hình chữ nhật
b) BK và NE cùng bằng hiệu khoảng cách từ M đến AC và AB (dù M thay đổi trên đường thẳng MC miễn là B nằm giữa M và C)
Phương pháp giải - Xem chi tiết
a) Tứ giác BKEN có ba góc bằng 90 o
b) Chứng minh ΔMBD = ΔMBN (cạnh huyền – góc nhọn)
Suy ra MD = MN
Lại có: BK = NE = ME – MN suy ra BK = NE = ME − MD.
Lời giải chi tiết
a) Xét tứ giác BKEN có: \(\widehat {BKE} = \widehat {KEN} = \widehat {ENB} = {90^o}\)
Suy ra tứ giác BKEN là hình chữ nhật
b) D là chân đường vuông góc hạ từ M đến AB
Ta có BN // AC (do BKNE là hình chữ nhật) suy ra \(\widehat {MBN} = \widehat {BCA}\)(hai góc đồng vị)
\(\widehat {MB{\rm{D}}} = \widehat {ABC}\) (đối đỉnh)
Mà \(\widehat {ABC} = \widehat {BCA}\) (tam giác ABC cân tại A) suy ra \(\widehat {MBN} = \widehat {MB{\rm{D}}}\)
Xét tam giác vuông MBD và MBN ta có:
BM chung
\(\widehat {MBN} = \widehat {MB{\rm{D}}}\)
Suy ra ΔMBD = ΔMBN (cạnh huyền – góc nhọn)
Suy ra MD = MN
Lại có: BK = NE = ME – MN suy ra BK = NE = ME − MD