Giải bài 3. 9 trang 34 sách bài tập toán 8 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

Cho tam giác ABC vuông cân tại đỉnh A. Ghép thêm vào phía ngoài tam giác đó tam giác BCD vuông cân tại đỉnh B. Chứng minh tứ giác ABDC là một hình thang vuông (hình thang có một cạnh bên vuông góc với đáy).

Lời giải chi tiết

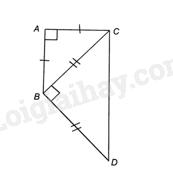
Do \(\Delta ABC\) vuông cân tại đỉnh A nên \(\widehat {ABC} = \widehat {ACB}\); \(\widehat A = 90^\circ \)

Xét trong \(\Delta ABC\) có \(\widehat {ABC} + \widehat {ACB} + \widehat A = 180^\circ \)

Nên \(\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ  - \widehat A}}{2} = \frac{{180^\circ  - 90^\circ }}{2} = 45^\circ \)

Tương tự do \(\Delta BCD\) vuông cân tại đỉnh B nên \(\widehat {BCD} = \widehat {BDC}\); \(\widehat {CBD} = 90^\circ \)

Xét trong \(\Delta BCD\) có \(\widehat {BCD} + \widehat {BDC} + \widehat {CBD} = 180^\circ \)

Nên \(\widehat {BCD} = \widehat {BDC} = \frac{{180^\circ  - \widehat {CBD}}}{2} = \frac{{180^\circ  - 90^\circ }}{2} = 45^\circ \).

Ta có \(\widehat {ABC} = 45^\circ  = \widehat {BCD}\) nên AB // CD (hai góc so le trong bằng nhau).

Vậy ABCD là một hình thang với AB, CD là hai đáy; cạnh bên của hình thang là AC vuông góc với đáy AB nên hình thang đó là hình thang vuông.