Giải bài 3. 14 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

Cho hình bình hành ABCD với góc A tù. Dựng bên ngoài hình bình hành đó các tam giác đều ABE và DAF. Chứng minh rằng tam giác CEF là tam giác đều.

( Gợi ý: Chứng minh các tam giác AEF, DCF, BEC bằng nhau)

Lời giải chi tiết

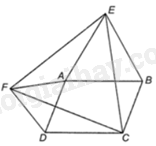
Vì ABCD là hình bình hành nên $AB = CD,AD = BC$, $\widehat {ADC} = \widehat {ABC} = {180^0} - \widehat {BAD}$

Vì $\Delta$ABE đều nên $AE = EB = AB$; $\widehat {EAB} = \widehat {ABE} = \widehat {AEB} = {60^0}$

Vì $\Delta$ADF đều nên $AD = DF = AF$; $\widehat {FAD} = \widehat {FDA} = \widehat {ADF} = {60^0}$

Ta có: $\widehat {FAE} = {360^0} - \widehat {EAB} - \widehat {DAB} - \widehat {FAD} = {240^0} - \widehat {DAB}$

$\widehat {FDC} = \widehat {FDA} + \widehat {ADC} = {60^0} + {180^0} - \widehat {DAB} = {240^0} - \widehat {DAB}$

Do đó, $\widehat {FAE} = \widehat {FDC}$

Tam giác AEF và tam giác DCF có:

$AF = DF\left( {cmt} \right),\widehat {FAE} = \widehat {FDC}\left( {cmt} \right),AE = DC\left( { = AB} \right)$

Suy ra $\Delta AEF = \Delta DCF\left( {c - g - c} \right)$, do đó, $FE = CF\left( 1 \right)$

Ta có: $\widehat {FDC} = \widehat {FDA} + \widehat {ADC} = {60^0} + \widehat {ABC} = \widehat {ABE} + \widehat {ABC} = \widehat {EBC}$

Tam giác EBC và tam giác FDC có:

$BC = DF\left( { = AD} \right),\widehat {EBC} = \widehat {FDC}\left( {cmt} \right),EB = DC\left( { = AB} \right)$

Suy ra $\Delta BEC = \Delta DCF\left( {c - g - c} \right)$, do đó, $EC = CF\left( 2 \right)$

Từ (1) và (2) ta có: $EC = CF = FE$ nên tam giác FEC đều.