Giải bài 3.19 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Cho tam giác ABC không vuông tại A. Dựng bên ngoài tam giác đó hai tam giác ABD, ACE vuông cân tại đỉnh A rồi dựng hình bình hành AEID.
Đề bài
Cho tam giác ABC không vuông tại A. Dựng bên ngoài tam giác đó hai tam giác ABD, ACE vuông cân tại đỉnh A rồi dựng hình bình hành AEID.
a) Chứng minh hai tam giác ABC và DAI bằng nhau.
b) Chứng minh đường thẳng AI vuông góc với BC.
c) Chứng minh đường thẳng BE vuông góc với đường thẳng CD.
d) Gọi K là trung điểm của BD, chứng minh \(KC = KI\) và KC vuông góc với KI
( Gợi ý: Chứng minh hai tam giác AKI và BKC bằng nhau).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có các cạnh đối bằng nhau và song song.
Lời giải chi tiết
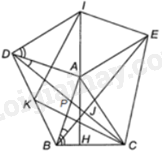
a) Vì AEID là hình bình hành nên \(\widehat {ADI} + \widehat {DAE} = {180^0}\) (hai góc kề một cạnh của hình bình hành)
Ta có: \(\widehat {DAE} + \widehat {DAB} + \widehat {BAC} + \widehat {CAE} = {360^0}\)
Mà tam giác ABD vuông tại A, tam giác ACE vuông tại A nên \(\widehat {BAC} + \widehat {DAE} = {360^0} - {90^0} - {90^0} = {180^0}\)
Do đó, \(\widehat {ADI} = \widehat {BAC}\)
Tam giác ABD vuông cân tại A nên \(AB = AD\)
Tam giác ACE vuông cân tại A nên \(AC = AE\)
Vì AEID là hình bình hành nên \(AE = DI\), do đó \(DI = AC\)
Tam giác ADI và tam giác BAC có:
\(AB = AD\)(cmt), \(\widehat {ADI} = \widehat {BAC}\) (cmt), \(DI = AC\) (cmt)
Do đó, \(\Delta ADI = \Delta BAC\left( {c - g - c} \right)\)
b) Giả sử AI cắt BC ở H.
Ta có: \(\widehat {DAI} + \widehat {DAB} + \widehat {BAH} = {180^0}\), mà \(\widehat {DAB} = {90^0}\) (do tam giác DAB vuông cân tại A). Suy ra \(\widehat {DAI} + \widehat {BAH} = {90^0}\)
Mà \(\widehat {DAI} = \widehat {ABC}\) (do \(\Delta ADI = \Delta BAC\)) nên \(\widehat {ABH} + \widehat {BAH} = {90^0}\)
Tam giác ABH có: \(\widehat {ABH} + \widehat {BAH} + \widehat {AHB} = {180^0}\) nên \(\widehat {AHB} = {180^0} - \left( {\widehat {ABH} + \widehat {BAH}} \right) = {90^0}\)
Do đó, AI vuông góc với BC tại H.
c) Ta có: \(\widehat {BAE} = \widehat {BAC} + \widehat {CAE} = \widehat {BAC} + {90^0}\)
\(\widehat {DAC} = \widehat {BAC} + \widehat {BAD} = \widehat {BAC} + {90^0}\)
Do đó, \(\widehat {BAE} = \widehat {DAC}\)
Tam giác BAE và tam giác DAC có:
\(AB = AD\left( {cmt} \right),\widehat {BAE} = \widehat {DAC}\left( {cmt} \right),AE = AC\left( {cmt} \right)\)
Do đó, \(\Delta BAE = \Delta DAC\left( {c - g - c} \right)\), suy ra \(\widehat {EBA} = \widehat {CDA}\)
Gọi J là giao điểm của DC và BE, ta có: \(\widehat {JBA} = \widehat {JDA}\)
Gọi P là giao điểm của AB và CD.
Tam giác ADP vuông tại A nên \(\widehat {PDA} + \widehat {DPA} = {90^0}\)
Mà \(\widehat {PDA} = \widehat {JBP},\widehat {DPA} = \widehat {BPJ}\) (đối đỉnh)
Do đó, \(\widehat {JBP} + \widehat {BPJ} = {90^0}\), suy ra \(\widehat {BJP} = {90^0}\) hay BE vuông góc với đường thẳng CD.
d) Tam giác ABD vuông cân tại A nên AK vừa là đường trung tuyến, vừa là đường cao, đường phân giác. Do đó, \(\widehat {DAK} = \frac{1}{2}\widehat {BAD} = {45^0}\)
Khi đó, \(\widehat {ABK} = \widehat {BAK} = {45^0}\) nên tam giác ABK vuông cân tại K, do đó, \(KA = KB\)
Ta có: \(\widehat {KAI} = \widehat {DAK} + \widehat {DAI} = {45^0} + \widehat {DAI} = {45^0} + \widehat {ABC}\)
Mặt khác \(\widehat {KBC} = \widehat {ABK} + \widehat {ABC} = {45^0} + \widehat {ABC}\)
Do đó, \(\widehat {KAI} = \widehat {KBC}\)
Tam giác AKI và tam giác BKC có:
\(AK = BK,\widehat {KAI} = \widehat {KBC},AI = BC\) (do \(\Delta ADI = \Delta BAC\))
Suy ra \(\Delta AKI = \Delta BKC\left( {c - g - c} \right)\) nên \(KI = KC\); \(\widehat {AKI} = \widehat {BKC}\)
Ta có: \(\widehat {AKC} + \widehat {BKC} = {90^0}\), mà \(\widehat {AKI} = \widehat {BKC}\) nên \(\widehat {AKC} + \widehat {AKI} = {90^0}\) hay \(\widehat {IKC} = {90^0}\) nên KC vuông góc với KI.