Giải bài 3. 22 trang 39 sách bài tập toán 8 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

1. Sử dụng tính chất tổng các góc của một tam giác bằng \({180^0}\) để chứng minh:

a) Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

b) Tam giác ABC có đường trung tuyến AM bằng nửa BC thì tam giác vuông tại A.

2. Sử dụng tính chất hai đường chéo của hình chữ nhật bằng nhau để chứng minh a), b) của ý 1.

Lời giải chi tiết

1.

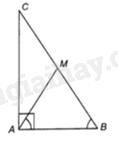
a) Giả sử tam giác ABC vuông tại A.

Do B là góc nhọn, lấy điểm M thuộc BC sao cho \(\widehat {BAM} = \widehat {ABM}\) nên tam giác ABM cân tại M. Do đó, \(AM = MB\)

Vì \(\widehat {BAM} + \widehat {MAC} = \widehat {ABM} + \widehat {ACM} = {90^0}\) nên \(\widehat {MAC} = \widehat {ACM}\), do đó, tam giác AMC cân tại M. Do đó, \(MA = MC.\)

Vậy \(MA = MB = MC = \frac{1}{2}BC\)

b) Ngược lại, nếu M thuộc BC sao cho \(MA = MB = MC = \frac{1}{2}BC\) thì tam giác MAB cân tại M, tam giác MAC cân tại M.

Suy ra, \(\widehat {MAB} = \widehat B,\widehat {MAC} = \widehat C\)

Ta có: \(\widehat {BAC} = \widehat {MAC} + \widehat {MAB}\)

Nên \(\widehat {BAC} = \widehat B + \widehat C\), mà \(\widehat {BAC} + \widehat B + \widehat C = {180^0}\) nên \(\widehat {BAC} = {90^0}\)

Do đó, tam giác ABC vuông tại A.

2.

Gọi M là trung điểm của BC, lấy điểm P sao cho M là trung điểm của AP thì tứ giác ABPC là hình bình hành.

a) Nếu tam giác ABC vuông tại A thì hình bình hành ABPC có \(\widehat {BAC} = {90^0}\) nên ABPC là hình chữ nhật. Do hai đường chéo AP, BC bằng nhau nên \(MA = MB = MC = MP\)

b) Nếu M thuộc BC sao cho \(MA = MB = MC = \frac{1}{2}BC\) thì suy ra \(BC = AP\). Khi đó, hình bình hành ABPC có hai đường chéo bằng nhau nên ABPC là hình chữ nhật. Do đó, \(\widehat {CAB} = {90^0}\)

Vậy tam giác ABC vuông tại A.