Giải bài 3. 18 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

Cho hình bình hành ABCD. Lấy các điểm E thuộc AB, F thuộc CD sao cho \(AE = CF\); lấy các điểm G thuộc BC, H thuộc AD sao cho \(BG = DH.\) Chứng minh EGFH là một hình bình hành và các đường thẳng AC, BD, EF, GH đồng quy.

Lời giải chi tiết

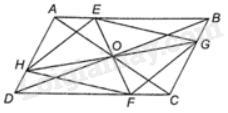
Vì ABCD là hình bình hành nên \(AB = CD,AD = BC,\) \(\widehat {ABC} = \widehat {ADC},\widehat {DAB} = \widehat {DCB}\)

Vì \(AB = CD\), \(AE = CF\) nên \(AB - AE = CD - FC\), suy ra \(EB = DF\)

Vì \(AD = BC\), \(DH = BG\) nên \(AD - DH = BC - BG\), suy ra \(AH = CG\)

Tam giác HEA và tam giác GCF có:

\(AE = CF\left( {gt} \right),\widehat {HAE} = \widehat {GCF}\left( {cmt} \right),AH = CG\left( {cmt} \right)\)

Do đó, \(\Delta HAE = \Delta GCF\left( {c - g - c} \right)\), suy ra \(HE = FG\)

Tam giác EBG và tam giác FDH có:

\(BG = DH\left( {gt} \right),\widehat {EBG} = \widehat {HDF}\left( {cmt} \right),EB = DF\left( {cmt} \right)\)

Do đó, \(\Delta EBG = \Delta FDH\left( {c - g - c} \right)\), suy ra \(GE = FH\)

Tứ giác EGFH có: \(HE = FG\), \(GE = FH\) nên EGFH là một hình bình hành.

Gọi O là trung điểm của AC.

Vì ABCD là hình bình hành nên hai đường chéo AC, BD cắt nhau tại O và O là trung điểm của BD (1).

Tứ giác EBFD có: EB//DF, \(EB = DF\)  nên tứ giác EBDF là hình bình hành. Do đó, hai đường chéo EF và BD cắt nhau tại trung điểm O của BD (2).

Vì tứ giác EGFH là hình bình hành nên hai đường chéo EF và GH cắt nhau tại trung điểm O của EF (3).

Từ (1), (2) và (3) ta có: Các đường thẳng AC, BD, EF, GH đồng quy tại O.