Giải bài 3 trang 10 SGK Toán 10 tập 2 – Chân trời sáng tạo

Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng

Đề bài

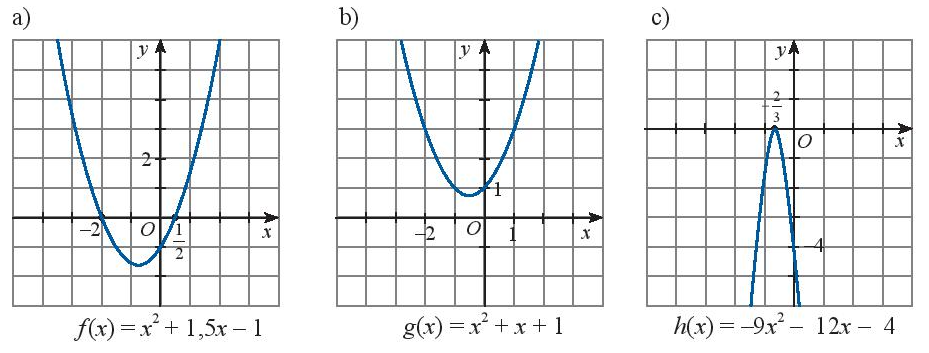
Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng

Phương pháp giải - Xem chi tiết

Bước 1: Xác định nghiệm của tam thức (là giao điểm của đồ thị với trục hoành)

Bước 2: Xác định khoảng mà \(f\left( x \right) > 0\) (khoảng đồ thị nằm trên trục hoành)

Bước 3: Xác định khoảng mà \(f\left( x \right) < 0\) (khoảng đồ thị nằm dưới trục hoành)

Bước 4: Lập bảng xét dấu

Lời giải chi tiết

a) Tam thức \(f\left( x \right) = {x^2} + 1,5x - 1\) có hai nghiệm phân biệt \({x_1} = - 2;{x_2} = \frac{1}{2}\)

\(\)\(f\left( x \right) > 0\) khi \(x \in \left( { - \infty , - 2} \right) \cup \left( {\frac{1}{2}, + \infty } \right)\) và \(f\left( x \right) < 0\) khi \(x \in \left( { - 2,\frac{1}{2}} \right)\)

Ta có bảng xét dấu như sau

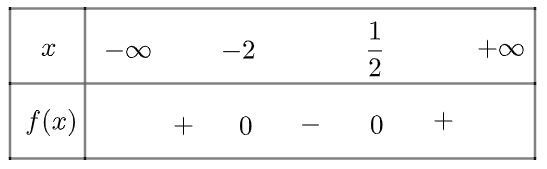
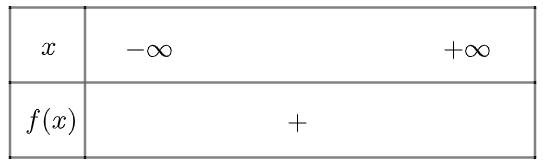
b) Tam thức \(g\left( x \right) = {x^2} + x + 1\) vô nghiệm, \(g\left( x \right) > 0\forall x \in \mathbb{R}\)

Ta có bảng xét dấu như sau

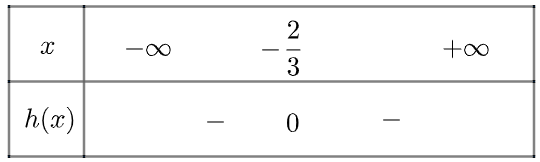
c) Tam thức \(h\left( x \right) = - 9{x^2} - 12x - 4\) có nghiệm kép \({x_1} = {x_2} = - \frac{2}{3}\) và \(h\left( x \right) < 0\forall x \ne - \frac{2}{3}\)

Ta có bảng xét dấu như sau

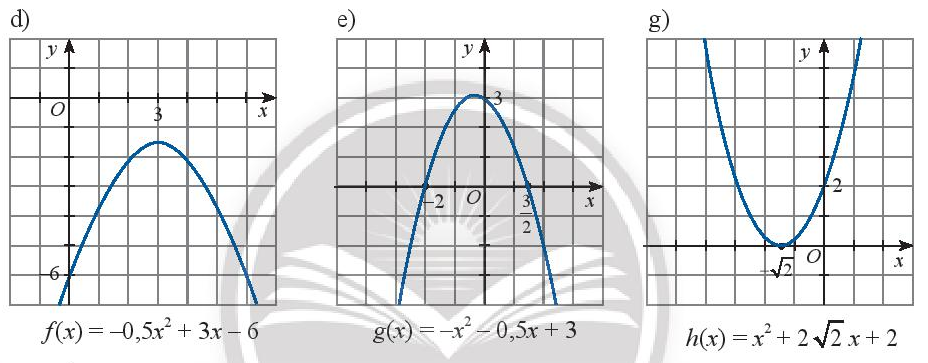
d) Tam thức \(f\left( x \right) = - 0,5{x^2} + 3x - 6\) vô nghiệm và \(f\left( x \right) < 0\forall x \in \mathbb{R}\)

Ta có bảng xét dấu như sau:

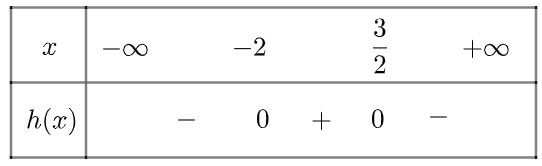
e) Tam thức \(g\left( x \right) = - {x^2} - 0,5x + 3\) có hai nghiệm \({x_1} = - 2,{x_2} = \frac{3}{2}\)

\(g\left( x \right) > 0\) khi \(x \in \left( { - 2,\frac{3}{2}} \right)\) và \(g\left( x \right) < 0\) khi \(x \in \left( { - \infty , - 2} \right) \cup \left( {\frac{3}{2}, + \infty } \right)\)

Ta có bảng xét dấu như