Giải bài 3 trang 100 SGK Toán 8 tập 1 - Cánh diều
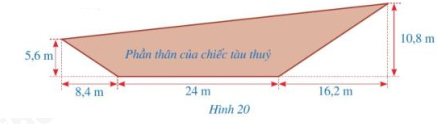
Hình 20 mô tả mặt cắt dọc phần nổi trên mặt nước của một chiếc tàu thủy.
Đề bài
Một chiếc tàu thủy có mặt cắt dọc phần nổi trên mặt nước của tân tàu được mô tả ở Hình 20. Tính chu vi mặt cắt dọc phần nổi trên mặt nước của thân tàu đó (làm tròn kết quả đến hàng phần mười của mét).
Phương pháp giải - Xem chi tiết
Ta đánh dấu các điểm của các tam giác vuông
Áp dụng định lí Pythagore để tính độ dài các cạnh.
Lời giải chi tiết
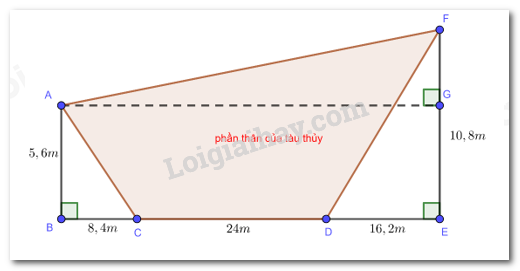
*) Áp dụng định lí Pythagore trong tam giác \(\Delta ABC\) vuông tại A có
\(A{C^2} = A{B^2} + B{C^2} = 5,{6^2} + 8,{4^2} = 101,92 \Rightarrow AC = \sqrt {101,92} \)
\(\Delta DEF\) vuông tại F có
\(D{F^2} = D{E^2} + E{F^2} = 16,{2^2} + 10,{8^2} = 379,08 \Rightarrow DF = \sqrt {379,08} \)
Kẻ \(AG \bot FG\)
Khi đó: \(FG = FE - GE = FE - AB = 10,8 - 5,6 = 5,2\)
Áp dụng định lí Pythagore trong \(\Delta AGF\) vuông tại G có
\(A{F^2} = A{G^2} + F{G^2} = 48,{6^2} + 5,{2^2} = 2389 \Rightarrow AF = \sqrt {2389} \)
Chu vi tứ giác ACDF là:
\(AC + CD + DF + AF = \sqrt {101,92} + \sqrt {379,08} + 24 + \sqrt {2389} \approx 102,4\)
Vậy chu vi của mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thủy là khoảng 102,4m.