Giải bài 3 trang 115 SGK Toán 8 tập 1 - Cánh diều — Không quảng cáo

Đề bài

Cho hình thoi ABCD có $\widehat {C{\rm{D}}B} = {40^o}$. Tính số đo mỗi góc của hình thoi ABCD.

Lời giải chi tiết

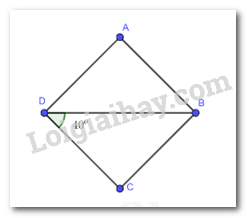
Do ABCD là hình thoi nên DB là tia phân giác của $\widehat {CDA}$

Mà: $\widehat {CDB} = {40^0} \Rightarrow \widehat {CDA} = {2.40^0} = {80^0} \Rightarrow \widehat {CBA} = \widehat {CDA} = {80^0}$

Mặt khác:

$\begin{array}{l}\widehat {BAD} + \widehat {CBA} + \widehat {CDA} + \widehat {BCD} = {360^0}\\\widehat {BAD} + {80^0} + {80^0} + \widehat {BCD} = {360^0}\end{array}$

(do ABCD là hình thoi nên $\widehat {BAD} = \widehat {BCD}$)

$\Rightarrow \widehat {BAD} = \widehat {BCD} = \frac{{{{360}^0} - {{80}^0} - {{80}^0}}}{2} = {100^0}$

Vậy hình thoi ABCD có: $\widehat {BCA} = \widehat {CDA} = {80^0};\widehat {BAD} = \widehat {BCD} = {100^0}$