Giải bài 3 trang 85 sách bài tập toán 9 - Cánh diều tập 2 — Không quảng cáo

Đề bài

Cho tam giác ABC cân tại A có O, I lần lượt là tâm các đường tròn ngoại tiếp và đường tròn nội tiếp tam giác ABC.

a) Chứng minh rằng:

- Ba điểm A, O, I cùng thuộc một đường thẳng;

- Đường thẳng OA vuông góc với BC và đi qua điểm chính giữa D (khác điểm A) của cung BC.

b) Cho BC = 24 cm, AC = 20 cm. Tính độ dài bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC.

Lời giải chi tiết

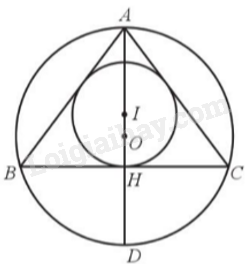
a) Gọi H là chân đường cao hạ từ A.

Tam giác ABC cân tại A, đường cao AH. Suy ra AH là đường trung tuyến của tam giác ABC.

Suy ra BH = HC. Vậy $OH \bot BC$(tính chất đường kính và dây cung).

Tương tự, ta có $IH \bot BC$ mà $AH \bot BC$nên A, O, I, H thẳng hàng hay cùng thuộc một đường thẳng.

Ta có A, O, I, H thẳng hàng mà $OH \bot BC$ nên $OA \bot BC$. Ta có AD là đường kính của đường tròn (O; OD) nên D cùng nằm trên đường thẳng A, I, O, H suy ra AD là đường trung trực của tam giác ABC. Vậy OA đi qua điểm chính giữa D (khác điểm A) của cung BC.

b) Do BC = 24 cm, AC = 20 cm nên ta có AH = $\sqrt {A{C^2} - H{C^2}}$ = 16 (cm).

Lại có $\Delta$ACH $\backsim$$\Delta$ADC nên AC ² = AH.AD, suy ra 20 ² = 16.AD hay AD = 25 cm.

Do đó R = AD : 2 = 12,5 cm.

Do BI là phân giác của góc ABH nên $\frac{{IH}}{{IA}} = \frac{{BH}}{{BA}} = \frac{{12}}{{20}} = \frac{3}{5}$.

Ta có $\frac{{IH}}{{IA}} = \frac{3}{5}$ hay $\frac{{IH}}{{IH + IA}} = \frac{3}{{3 + 5}} = \frac{3}{8}$, tức là $\frac{r}{{16}} = \frac{3}{8}$. Vì vậy r = 6 cm.