Giải bài 3 trang 88 vở thực hành Toán 9 tập 2
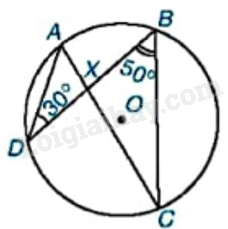
Cho đường tròn (O) và hai dây cung AC, BD cắt nhau tại X như hình bên. Tính số đo góc AXB biết rằng (widehat {ADB} = {30^o},widehat {DBC} = {50^o}).
Đề bài
Cho đường tròn (O) và hai dây cung AC, BD cắt nhau tại X như hình bên. Tính số đo góc AXB biết rằng \(\widehat {ADB} = {30^o},\widehat {DBC} = {50^o}\).
Phương pháp giải - Xem chi tiết
+ Do \(\widehat {DAC}\) và \(\widehat {DBC}\) là góc nội tiếp cùng chắn cung DC của (O) nên \(\widehat {DAC} = \widehat {DBC}\).
+ Vì tổng ba góc trong tam giác ADX bằng \({180^o}\) và góc AXB kề bù với góc AXD nên
\(\widehat {AXB} = {180^o} - \widehat {AXD} = \widehat {XAD} + \widehat {ADX}\).
Lời giải chi tiết
Do \(\widehat {DAC}\) và \(\widehat {DBC}\) là góc nội tiếp cùng chắn cung DC của (O) nên \(\widehat {DAC} = \widehat {DBC} = {50^o}\).
Vì tổng ba góc trong tam giác ADX bằng \({180^o}\) và góc AXB kề bù với góc AXD nên
\(\widehat {AXB} = {180^o} - \widehat {AXD} = \widehat {XAD} + \widehat {ADX} = {30^o} + {50^o} = {80^o}\).