Giải bài 4. 24 trang 63 sách bài tập toán 11 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

Cho tứ diện ABCD. Gọi G và H lần lượt là trọng tâm của hai tam giác ABC và ACD. Chứng minh rằng GH//(BCD)

Lời giải chi tiết

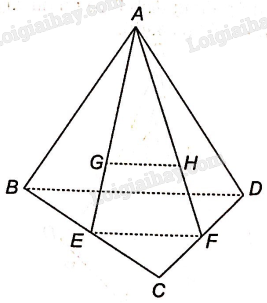
Gọi E, F lần lượt là trung điểm của các cạnh BC, CD. Vì G là trọng tâm của tam giác ABC nên A, G, E thẳng hàng và $\frac{{AG}}{{AE}} = \frac{2}{3}$

Tương tự ta có A, H, F thẳng hàng và $\frac{{AH}}{{AF}} = \frac{2}{3}.$

Do đó, $\frac{{AG}}{{AE}} = \frac{{AH}}{{AF}}$

Trong tam giác AEF có: $\frac{{AG}}{{AE}} = \frac{{AH}}{{AF}}$, theo định lí Thalès đảo ta có GH//EF, mà $EF \subset \left( {BCD} \right)$ nên GH//(BCD)